Матрица в excel

Содержание:

3 .6. Установка надстроек
Заключение
Вычисление обратной матрицы в Microsoft Excel
2.2. Создание и изменение формул массива
Синтаксис формулы массива
Пример функции МОПРЕД для вычисления детерминанта матрицы в Excel
Формулы массива
2.7. Регрессия
3 .5 . Надстройки
Функции массивов
Выполнение расчетов
3 .3 . Пример макроса
Изменение содержимого массива
Что можно делать с матрицами
- Транспонирование
Решение уравнений методом подбора параметров Excel
Нахождение обратной матрицы с помощью элементарных преобразований (метод Гаусса)
Матрицы в экселе
Анализ данных с помощью формулы массива

3 .6. Установка надстроек

Прежде чем начать использовать надстройку, нужно
выполнить процедуру ее установки
, которая состоит из двух частей.

В первой фазе файлы, входящие в пакет надстройки
размещают на компьютере. В некоторых пакетах имеется программа
Setup.exe, которая выполняет это автоматически. В других файлы нужно
размещать самостоятельно. Объясним, как это нужно сделать. В состав
пакета обязательно входит файл с расширением XLA и несколько
вспомогательных файлов с расширениями DLL, HLP и др. Все вспомогательные
файлы должны размещаться в следующих директориях:
C:\Windows
, или C:\Windows\System или
C:\Windows\System32
. Основной файл (с расширением XLA) может, в
принципе, находится в любом месте, но две директории являются
предпочтительными.

Microsoft рекомендует размещать файлы XLA в директории
C:\Documents and Settings\User\Application
Data\Microsoft\AddIns
, где User
– это
имя, под которым происходит вход в систему. Тогда этот файл можно быстро
загрузить на второй фазе установки. Однако, если рабочие книги
используются на нескольких компьютерах, с разными именами
User
, то, при смене компьютера, связи с
основным файлом надстройки теряются и их приходится
обновлять .

Поэтому мы предлагаем поместить файл
Chemometrics.xla
в директорию, которая имеет одно и то же имя на
разных компьютерах, например C:\Program
Files\Chemometrics
. Автоматическая установка надстройки
Chemometrics Add-In

описана .

Вторая фаза проводится из открытой книги Excel. В версии
2003 нужно выполнить последовательность команд
Tools-Add-Ins
, а в версии 2007 последовательность:
Office Button-Excel Options-Add-Ins-Go
. В
появившемся окне (см Рис. 45
) нужно нажать Browse
и найти в компьютере нужный файл XLA.

Рис.45
Установка надстройки

После того, как надстройка установлена, ее можно
активировать и деактивировать устанавливая отметку напротив имени. Для
удаления надстройки нужно снять галочку против ее имени в окне
Add-Ins
, закрыть Excel и удалить все ранее
установленные файлы с компьютера.

Заключение

Извлечение корня любой степени в ms excel 2010

Мы рассмотрели основные приемы работы с матрицами в
системе Excel

За рамками пособия осталось еще много всего важного.
Частично заполнить эти пробелы поможет пособие. В программе Excel с матрицей можно работать как с диапазоном

То есть совокупностью смежных ячеек, занимающих прямоугольную область

В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.

Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.

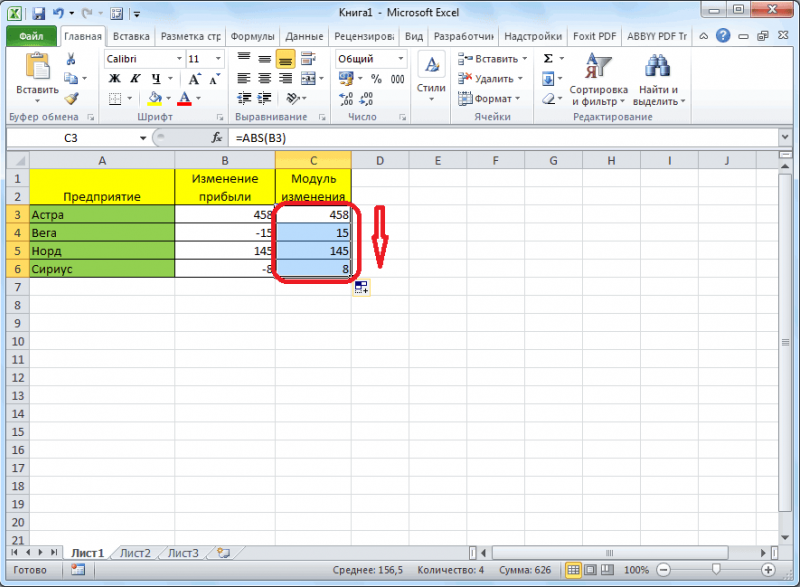
Вычисление обратной матрицы в Microsoft Excel

Excel разбить объединенные ячейки в excel

Приложение Excel выполняет целый ряд вычислений, связанных с матричными данными. Программа обрабатывает их, как диапазон ячеек, применяя к ним формулы массива. Одно из таких действий – это нахождение обратной матрицы. Давайте выясним, что представляет собой алгоритм данной процедуры.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.

1. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».

1. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».

Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.

1. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».

1. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».

1. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.

Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи.

Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

2.2. Создание и изменение формул массива

Перемножение одной матрицы на другую в microsoft excel

Для того чтобы правильно ввести формулу массива, нужно
выделить на листе область, размеры которой совпадают с ожидаемым
результатом.

Если выделить слишком большую область, то при вычислении
избыточные ячейки будут заполнены символами ошибки
#N/A. Если область вывода будет меньше, чем нужно, то часть
результатов пропадет. После выделения области, в
Formula Bar записывается
формула и нажимается CTRL+SHIFT+ENTER.

Альтернативно, сначала можно ввести формулу в одну
ячейку, затем отметить область вывода, начиная с этой ячейки (право и
вниз), потом перейти в Formula Bar и нажать
CTRL+SHIFT+ENTER.

Для того, чтобы изменить формулу массива нужно выделить
область содержащую результат. Затем нужно перейти
Formula Bar. При этом фигурные скобки вокруг формулы
{ } исчезнут. После этого формулу можно
изменить и нажать CTRL+SHIFT+ENTER.

Для того чтобы расширить область, которую занимает
формула массива, достаточно выделить для нее новую область, перейти в
Formula Bar и нажать CTRL+SHIFT+ENTER. А вот для того, чтобы уменьшить эту область
(например, чтобы избавиться от символов #N/A)
придется потратить больше сил. Сначала нужно встать на любую ячейку
области, перейти в Formula Bar и скопировать
строку формулы. Затем нужно стереть содержимое старой области и отметить
новую, меньшую область. После этого опять перейти в
Formula Bar, вставить формулу и нажать CTRL+SHIFT+ENTER.

Изменять отдельные ячейки в формуле массива нельзя. При
попытке сделать это появляется предупреждение .

Рис.27 Предупреждение о недопустимой операции с формулой массива

Синтаксис формулы массива

Давайте представим, что у нас есть таблица, в которой есть набор ячеек, а сумма к оплате описывается в одной ячейке. Для первого будем искать промежуточные итоги. Во втором же случае будем рассчитывать итоговую сумму.

Для начала нам нужно выделить диапазон, к какому в дальнейшем будет применена формула. В нашем случае это набор ячеек, начинающийся E3, а заканчивающийся E8.

Затем ставим курсор в строку формул, и там записываем =C3:C8*D3:D8.

Превращаем формулу в формат массива. Нужно нажать Ctrl + Shift + Enter.

После этого мы получаем таблицу с готовыми промежуточными итогами.

Как видим, после совершения этих операций формула облачилась в фигурные скобки. Именно они и говорят о том, что эта функция будет обрабатываться, как формула массива. Видим, что каждая ячейка каждого ряда превратилась в готовый результат.

Если попробовать внести какие-угодно изменения в результирующую ячейку, то появится такое уведомление о том, что операция запрещена.

Давайте приведем еще один вариант использования формулы массива. На этот раз мы выведем только одно результирующее значение в итоговую ячейку. Чтобы достичь этой цели, необходимо выполнить следующие действия.

Выделяем ту ячейку, которая будет содержать результат вычисления по формуле массива.
Вводим туда формулу. В нашем случае мы будем суммировать значения из целевого диапазона, поэтому используем формулу СУММ(C3:C8*D3:D8).
С использованием комбинации Ctrl + Shift + Enter осуществляем трансформацию стандартной формулы в ту, которая работает с массивами данных.

По итогу, получаем следующий результат.

В случае, если бы мы не знали, как правильно использовать формулы массива, нам бы пришлось использовать две обычные. А так мы избавлены от этой необходимости.

Давайте более подробно рассмотрим синтаксис этой формулы.

В нашем случае были использованы одномерные массивы. Формула обрабатывает каждый, после чего выполняет необходимые результаты, а итог выводит в ячейку.

Составные части формул массива:

Функция массива. Это описание той операции, которую Эксель должен выполнить.
Массивы диапазона. Это непосредственно те диапазоны, которые будут обрабатываться формулой.
Оператор массива – знак двоеточия. Обозначает расстояние в определенное количество ячеек между конкретными адресами.

Чтобы было проще понять, вот небольшой рисунок.

Пример функции МОПРЕД для вычисления детерминанта матрицы в Excel

Примеры использования функции МОПРЕД в Excel.

Пример 1. Одним из свойств матриц является то, что определитель (детерминант) исходной матрицы соответствует определителю транспонированной матрицы. Доказать справедливость этого суждения с использованием средств Excel.

Вид таблицы с данными:

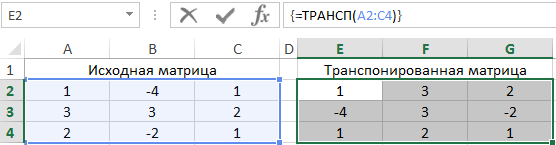
Для получения транспонированной матрицы выделим соответствующий по количеству строк и столбцов диапазон ячеек и используем следующую формулу (формула массива CTRL+SHIFT+Enter):

=ТРАНСП(A2:C4)

A2:A4 – диапазон ячеек со значениями исходной матрицы.

В результате получим:

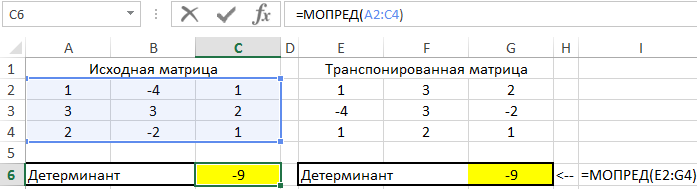
Рассчитаем детерминант для каждой матрицы отдельно:

=МОПРЕД(A2:C4)

=МОПРЕД(E2:G4)

A2:C4 и E2:G4 – диапазоны ячеек со значениями исходной и транспонированной матриц соответственно.

Полученные результаты:

Во избежание промежуточных вычислений можно было использовать формулу массива CTRL+SHIFT+Enter:

=МОПРЕД(ТРАНСП(A2:C4))

Результат вычислений:

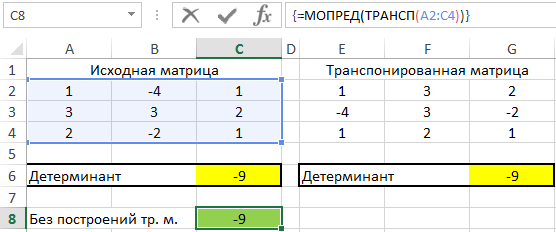
В результате вычислений формул Excel детерминант – доказан!

Формулы массива

В подавляющем количестве задач при работе с массивами (а матрицы и являются таковыми) используются формулы соответствующего типа. Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:

Выделить набор ячеек, где будут выводиться значения.
Непосредственно введение формулы.
Нажатие последовательности клавиш Ctrl + Shift + Ввод.

После осуществления этих простых действий в поле ввода отображается формула массива. Ее можно отличить от обычной по фигурным скобкам.

Для редактирования, удаления формул массива, надо выделить требуемый диапазон и сделать то, что нужно. Чтобы редактировать матрицу, нужно использовать ту же комбинацию, что и для ее создания. При этом нет возможности редактировать отдельный элемент массива.

2.7. Регрессия

Для построения используются
несколько стандартных функций листа.

TREND / ТЕНДЕНЦИЯ

Строит

y=b+m₁x₁+…+m_J x_J+e

Аппроксимирует известные значения вектора откликов
known_y’s для заданных значений матрицы предикторов
known_x’s и возвращает значения y,
для заданного массива new_x’s.

Синтаксис

TREND(known_y’s
)

Примечания

Вектор
known_y’s должен занимать один столбец,
тогда каждый столбец матрицы массива known_x’s
интерпретируется как отдельная переменная;
Если
аргумент known_x’sопущен, то предполагается, что это вектор чисел {1;2;3;…}
такого же размера, как и known_y’s;
Матрица
новых значений new_x’sдолжна иметь столько же столбцов
(переменных), как и матрица known_x’s;
Если
аргумент new_x’sопущен, то предполагается, что он совпадает с
массивом known_x’s.
Результат является вектором, в котором число строк равно
числу строк в массиве new_x’s.

Пример

Рис.34 ФункцияTREND

Функция TRENDявляется функцией
массива и ее ввод должен завершаться нажатием комбинации
CTRL+SHIFT+ENTER.

LINEST /
ЛИНЕЙН

Дополняет функцию TREND и выводит некоторые
статистические значения, связанные с регрессией

y=b+m₁x₁+…+m_J x_J+e

Синтаксис

LINEST(known_y’s
)

Рис. 35 Таблица вывода функция LINEST

m_J, …,
m₂, m₁
и b – оценки регрессионных
коэффициентов;

s_J, …,
s₂, s₁
и s_b
– стандартные ошибки для оценок регрессионных коэффициентов;

R2 –
коэффициент детерминации;

s_y –
стандартная ошибка оценки y;

F – F-статистика;

DoF – число степеней
свободы;

SS_reg –
регрессионная сумма квадратов;

SS_res–
остаточная сумма квадратов.

Примечания

LINEST – это
очень плохо сконструированная функция, очень неудобная в
практическом применении;
Примечания,
представленные в описании функции полностью применимы к
функции LINEST.

Пример

Рис.36 ФункцияLINEST

Функция LINEST является функцией массива и ее ввод должен
завершаться нажатием комбинации CTRL+SHIFT+ENTER.

3 .5 . Надстройки

Написанные пользователем программы хранятся в той книге
Excel, в которой они были созданы, в ее специальных разделах, называемых
модулями
. Для того чтобы эти макросы были доступны в других
книгах, их можно туда скопировать, но можно поступить и по-другому –
создать надстройку.

Надстройка
– это специальный файл Excel,
содержащий в себе несколько VBA модулей, связанных со всеми
необходимыми библиотеками DLL. Надстройку можно подключить к системе
Excel для расширения ее возможностей.

Стандартная версия Excel включает несколько надстроек,
среди которых для нас примечательны две: Solver Add-In и Analysis
Toolpak.

Функции массивов

Наиболее удобно в качестве формул использовать уже готовые встроенные функции Excel. Доступ к ним можно получить через Мастер функций, нажав кнопку «Вставить функцию» слева от строки формул. Или же во вкладке «Формулы» на ленте можно выбрать одну из категорий, в которой находится интересующий вас оператор.

После того, как пользователь в Мастере функций или на ленте инструментов выберет наименование конкретного оператора, откроется окно аргументов функции, куда можно вводить исходные данные для расчета.

Правила ввода и редактирования функций, если они выводят результат сразу в несколько ячеек, те же самые, что и для обычных формул массива. То есть, после ввода значения обязательно нужно установить курсор в строку формул и набрать сочетание клавиш Ctrl+Shift+Enter.

Урок: Мастер функций в Excel

Оператор СУММ

Одной из наиболее востребованных функций в Экселе является СУММ. Её можно применять, как для суммирования содержимого отдельных ячеек, так и для нахождения суммы целых массивов. Синтаксис этого оператора для массивов выглядит следующим образом:

Данный оператор выводит результат в одну ячейку, а поэтому для того, чтобы произвести подсчет, после внесения вводных данных достаточно нажать кнопку «OK» в окне аргументов функции или клавишу Enter, если ввод выполнялся вручную.

Урок: Как посчитать сумму в Экселе

Оператор ТРАНСП

Функция ТРАНСП является типичным оператором массивов. Она позволяет переворачивать таблицы или матрицы, то есть, менять строки и столбцы местами. При этом она использует исключительно вывод результата в диапазон ячеек, поэтому после введения данного оператора обязательно нужно применять сочетание Ctrl+Shift+Enter. Также нужно отметить, что перед введением самого выражения нужно выделить на листе область, у которой количество ячеек в столбце будет равно числу ячеек в строке исходной таблицы (матрицы) и, наоборот, количество ячеек в строке должно равняться их числу в столбце исходника. Синтаксис оператора следующий:

Урок: Транспонирование матриц в Excel

Урок: Как перевернуть таблицу в Экселе

Оператор МОБР

Функция МОБР позволяет производить вычисление обратной матрицы. Все правила ввода значений у этого оператора точно такие же, как и у предыдущего

Но важно знать, что вычисление обратной матрицы возможно исключительно в том случае, если она содержит равное количество строк и столбцов, и если её определитель не равен нулю. Если применять данную функцию к области с разным количеством строк и столбцов, то вместо корректного результата на выходе отобразится значение «#ЗНАЧ!»

Синтаксис у этой формулы такой:

Для того чтобы рассчитать определитель, применяется функция со следующим синтаксисом:

Урок: Обратная матрица в Excel

Как видим, операции с диапазонами помогают сэкономить время при вычислениях, а также свободное пространство листа, ведь не нужно дополнительно суммировать данные, которые объединены в диапазон, для последующей работы с ними. Все это выполняется «на лету». А для преобразования таблиц и матриц только функции массивов и подходят, так как обычные формулы не в силах справиться с подобными задачами. Но в то же время нужно учесть, что к подобным выражениям применяются дополнительные правила ввода и редактирования.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Выполнение расчетов

Расчет определителя

Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.

Прежде всего, уясним одно правило: Матрица имеет обратную только тогда, когда ее определитель не равен нулю. А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1. Нажимаем Формулы, затем Математические и в появившемся окне находим МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК. В ячейке, которую мы застолбили под ответ, появилось число 3, Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2, а затем на одновременно на три клавиши Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица

3 .3 . Пример макроса

Второй способ опирается на рекуррентное соотношение,
связывающее два соседних члена в ряду

Для того чтобы воспользоваться этим соотношением, надо
организовать на листе рекуррентную процедуру. Например, так, как
показано на Рис. 42

Рис.42
Вычисление функции E
1 (x
)
итерационным способом

Один шаг итерации – это переход от значений в области
J2:J4
к значениям в области
L2:L4
. Для того, чтобы сделать следующую
итерацию, нужно скопировать значения, получившиеся в области
L2:L4
и вставить их в область
J2:J4
. При этом вставлять нужно только
величины, без формул. Величины в области H2:H4

дают исходные значения для начала итерации.Повторяя многократно
операцию Copy-Paste Special
, можно получить в
ячейке L4
искомое значение. Однако
копирование – это скучное занятие и его было бы неплохо
автоматизировать. Для этого можно написать макрос.

Проще всего начать создание макроса через запись команд,
выполняемых на листе. Для этого идем в раздел меню Tools–Macro–Record
New Macro
. Появляется окно (Рис. 43
), в котором можно указать имя
макроса и где он будет расположен.

Рис.43
Запись макро

После нажатия OK
начинается
запись всех действий, выполняемых на листе. Когда все, что нужно
сохранено в макросе, запись надо остановить командой
Tools–Macro–Stop Recording
. Результат можно увидеть, зайдя в
редактор Visual Basic

.

Рис.44
Редактор Visual Basic

На Рис.

Рис.45
Функция IntExp

На Рис. 45
приведен
код этой функции и пример обращения к
ней.

Мы не будем рассказывать о программировании на VBA, т.к.
это очень большой и сложный вопрос. Самостоятельно его можно изучить по
имеющимся в сети многочисленным пособиям, например,
.

VBA – это довольно медленный язык и он плохо подходит
для больших вычислений. Например, не стоит писать на этом языке
процедуру для PCA декомпозиции – на больших массивах она будет считать
очень долго. Правильнее рассматривать Excel и VBA как интерфейс (front
end) для ввода и вывода данных, которые затем передаются в динамическую
библиотеку (DLL), написанную на быстром языке, таком как C++ (back end).
Именно эта концепция и была реализована в надстройках
Fitter
и
Chemometrics
.

Подробнее об использовании пользовательских функций для
расширения возможностей надстройки Chemometrics

можно прочитать
.

Изменение содержимого массива

Новички нередко сталкиваются с трудностями в попытках изменить часть массива, потому что каким бы способом они не пытались бы выкрутиться, Эксель все равно показывает сообщение, что это сделать нельзя. Тем не менее, все гениальное просто. В этом случае – также. Достаточно просто выполнить несколько элементарных действий:

Найти кнопку «Отмена», расположенную слева от строки формул. Еще один вариант – нажатие клавиши Esc, которая выполняет ту же операцию. Во всех случаях блокировка будет снята и все операции можно выполнять заново.
Снова ввести формулу массива с тем же диапазоном.

Таким образом, изменение содержимого массива возможно лишь если все отменить, а потом заново вводить формулу. Неудобно, конечно, но значительно удобнее, чем использовать стандартные формулы.

Что можно делать с матрицами

В целом, есть огромное количество действий, применение которых возможно для матриц. Давайте каждое из них рассмотрим более подробно.

Транспонирование

Многие люди не понимают значения этого термина. Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием.

Перед тем, как это осуществить, необходимо выделить отдельную область, которая имеет такое же количество строчек, сколько столбцов есть у исходной матрицы и такое же количество столбцов. Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.

Далее есть несколько методов, как можно осуществить транспонирование.

Первый способ следующий. Для начала нужно выделить матрицу, после чего скопировать ее. Далее выделяется диапазон ячеек, куда должен быть вставлен транспонированный диапазон. Далее открывается окно «Специальная вставка».

Там есть множество операций, но нам нужно найти радиокнопку «Транспонировать». После совершения этого действия нужно подтвердить его нажатием клавиши ОК.

Есть еще один способ, с помощью которого можно транспонировать матрицу. Сперва надо выделить ячейку, расположенную в верхнем левом углу диапазона, отведенного под транспонированную матрицу. Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП. Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.

После нажатия кнопки ОК сначала будет показано, что вы допустили ошибку. Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:

Выделить набор ячеек, отведенных под транспонированную матрицу.
Нажать клавишу F2.
Нажать на горячие клавиши Ctrl + Shift + Enter.

Главное достоинство метода заключается в способности транспонированной матрицы сразу корректировать содержащуюся в ней информацию, как только вносятся данные в изначальную. Поэтому рекомендуется использовать именно данный способ.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

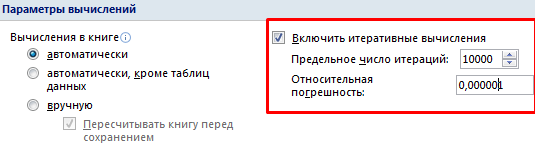
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».

Нахождение обратной матрицы с помощью элементарных преобразований (метод Гаусса)

Пример 3. Методом элементарных преобразований вычислить -1 если = .

Решение. Приписываем к исходной справа единичную того же порядка: . С помощью элементарных преобразований столбцов приведём левую “половину” к единичной, совершая одновременно точно такие преобразования над правой «половиной».
Поменяем местами 1 со 2 столбцы: ~. К третьему прибавим первый, ко второму — первый, × на -2: . Из первого вычтем удвоенный второй, из третьего — × на 6 второй; . Прибавим третий к первому и второму: . Умножим последний на минус один: . Справа от вертикальной черты квадратная таблица размером 3х3 .

Матрицы в экселе

В разделе Прочее компьютерное на вопрос Как создать матрицу в Excel???? заданный автором Masha Kalganova лучший ответ это Что конкретно нужно сделать?Документ эксель — безразмерная (всеразмерная) матрица, каждый элемент которой может быть числом, текстом или любым другим значением. Да хоть формулой.Если напечатать 3 циферки в ряд, под ними еще 3 в ряд, под ними еще 3 в ряд, получим квадратную матрицу 3х3.Вопрос в чем?Умножение матрицы на число в ExcelФормулы написать?В верхней левой клетке новой матрицы=левая верхняя клетка старой матрицы * клетка с числом (ткнуть мышкой) , нажать F4 дабы стало $x$y, где x,y — координаты клетки. Это зафиксирует клетку при копировании. Далее жмем Enter и копируем содержимое клетки в 2 соседние клетки в ряд. Далее копируем эти 3 клетки в следующие 3 ряда и получаем тот же результат, что у меня на картинке. То есть умножение матрицы на число.Блин, математику не знают, а в интернете лазают!

Ответ от Serg Kчто такое «матрица»? выражайся яснее, Маша.

Анализ данных с помощью формулы массива

Формулы массива очень удобно использовать, если стоит задача анализировать информацию. В частности, можно проверять ее на предмет соответствия определенному критерию. Допустим, у нас есть такая таблица, в которой описываются продажи разными менеджерами. В одном отделе работает три сотрудника, а также продается три вида товаров. Ну и наконец, каждый из них имеет свою цену, а итоговая стоимость записывается в третьей колонке таблицы.

Перед нами стоит задача определить, насколько каждый из менеджеров является эффективным, учитывая продаваемые ими товары. Это можно сделать и самостоятельно, но с помощью формулы массива данную задачу можно выполнить буквально в несколько кликов.

Давайте запишем в подходящих ячейках информацию, которая будет служить критерием для оценки эффективности. В нашем случае это товар и идентификатор менеджера, которого мы проверяем.

Чтобы успешно решить эту задачу, достаточно просто воспользоваться небольшой формулой массива.

Конечная наша цель – получение суммы, поэтому нужно использовать соответствующую функцию. Кроме этого, нам надо применить условие, на соответствие которым будет проверяться диапазон.

В результате получится формула, приведенная на скриншоте.

В ней используется 3 множителя. Первый проверяет менеджеров. Второй – товары. А третий – непосредственно определяет сумму заказа.

Как работает эта формула? Да очень просто. Ее алгоритм следующий:

Сначала Excel проверяет всех менеджеров и товары, соответствуют ли они заданным критериям. Если да, функция возвращает значение 1, если нет – 0.
В случае несоответствия значений хотя бы одному из условий, один из множителей становится равным нулю. Соответственно, и итоговый результат будет аналогичным.
Если же оба условия выполняются, то функция осуществляет операцию умножения.
Наконец, все полученные значения суммируются, после чего ячейка выдает общую эффективность по обработанным заказам.

Вот таким образом можно простую формулу использовать, чтобы выполнять даже самую сложную обработку информации. В конечном итоге, можно несколько модернизировать отчет, добавив выпадающий список, в котором выбираются товары и менеджеры. Но это уже совсем другая тема.