Создание и импорт модулей

Импорт модуля

Если запустить в каталоге, в котором лежит данный модуль (например, my_module.py), интерпретатор:

>>> python

и потом сделать импорт модуля:

>>> import my_module

то мы получаем доступ ко всем функциям, которые в модуле определены:

>>> my_module.func1()
>>> my_module.func2()
...

Для более короткой записи можно создать локальную переменную:

>>> f1 = my_module.func1

Второй вариант импорта — взятие непосредственно имени без имени модуля:

>>> from my_module import func1, func2
>>> func1()

Третий вариант импорта — включение всех имен, определенных в модуле:

>>> from my_module import *
>>> func1()

Для предотвращения конфликта имен можно использовать создание алиаса:

>>> from my_module import open as my_open

Пример. Импорт на основе from обладает такой особенностью, что он делает импортируемые атрибуты read-only:

>>> from small import x, y
>>> x = 42

В данном случае x — это локальная переменная, в то время как переменные x, y в самом модуле small не меняются:

>>> import small
>>> small.x = 42

здесь x — глобальная переменная.

Во избежание недоразумений import предпочтительнее без from в тех случаях, когда один и тот же модуль используется в нескольких местах.

Поскольку модуль загружается один раз, для его повторной загрузки можно использовать функцию reload().

Каждый модуль имеет собственное пространство имен, являющееся глобальной областью видимости для всех определенных в нем функций. Для того чтобы переменные этого модуля не попали в конфликт с другими глобальными именами или другими модулями, нужно использовать префикс: _имя_модуля_._имя_переменной_ .

Модули могут импортировать другие модули. Обычно инструкцию import располагают в начале модуля или программы.

Создать комбинации с помощью combinations()

Мы также можем создавать последовательности комбинаций, используя Python .

iterator = itertools.combinations(*sequence, r)

Вот простой пример:

import itertools
words = 
results = itertools.combinations(words, 2)
for item in results:
    print(item)

Выход

('hello', 'from')
('hello', 'AskPython')
('hello', 'how')
('from', 'AskPython')
('from', 'how')
('AskPython', 'how')

Если вы хотите, чтобы в комбинациях повторялись последовательные элементы, вы можете использовать .

results = itertools.combinations_with_replacement(words, 3)

for item in results:
    print(item)

Выход

('hello', 'hello', 'hello')
('hello', 'hello', 'from')
('hello', 'hello', 'AskPython')
('hello', 'hello', 'how')
('hello', 'from', 'from')
('hello', 'from', 'AskPython')
('hello', 'from', 'how')
('hello', 'AskPython', 'AskPython')
('hello', 'AskPython', 'how')
('hello', 'how', 'how')
('from', 'from', 'from')
('from', 'from', 'AskPython')
('from', 'from', 'how')
('from', 'AskPython', 'AskPython')
('from', 'AskPython', 'how')
('from', 'how', 'how')
('AskPython', 'AskPython', 'AskPython')
('AskPython', 'AskPython', 'how')
('AskPython', 'how', 'how')
('how', 'how', 'how')

Точно так же вы можете перечислить перестановки, используя и .

Графический интерфейс

В стандартной библиотеке Python есть
графическая библиотека интерфейсов
Tkinter. Но при помощи внешних модулей вы
можете поднять GUI ваших приложений на
новый уровень.

wxPython. Создает по-настоящему нативные пользовательские интерфейсы для Python-приложений, которые могут запускаться на Windows, Mac и Linux, а также прочих Unix-подобных системах практически без каких-либо модификаций.

PyGObject. Пакет Python, предоставляющий привязки для библиотек на базе Gobject, таких как GTK, GStreamer, WebKitGTK, GLib, GIO и др.

Pmw. Набор инструментов для создания на Python высокоуровневых составных виджетов (с использованием модуля Tkinter).

WCK. Расширение API, позволяющее реализовывать на чистом Python всевозможные пользовательские виджеты.

Tix. Мощный набор компонентов пользовательского интерфейса, при помощи которого можно расширить возможности ваших Tcl/Tk и Python-приложений. Использование Tix вместе с Tk очень улучшает внешний вид и функционал приложений.

Гиперболические функции

Подобно тригонометрическим функциям, гиперболические функции для комплексного числа также доступны в модуле .

import cmath

a = 3 + 4j

print('Hyperbolic Sine:', cmath.sinh(a))
print('Hyperbolic Cosine:', cmath.cosh(a))
print('Hyperbolic Tangent:', cmath.tanh(a))

print('Inverse Hyperbolic Sine:', cmath.asinh(a))
print('Inverse Hyperbolic Cosine:', cmath.acosh(a))
print('Inverse Hyperbolic Tangent:', cmath.atanh(a))

Вывод:

Hyperbolic Sine: (-6.5481200409110025-7.61923172032141j)
Hyperbolic Cosine: (-6.580663040551157-7.581552742746545j)
Hyperbolic Tangent: (1.000709536067233+0.00490825806749606j)
Inverse Hyperbolic Sine: (2.2999140408792695+0.9176168533514787j)
Inverse Hyperbolic Cosine: (2.305509031243477+0.9368124611557198j)
Inverse Hyperbolic Tangent: (0.11750090731143388+1.4099210495965755j)

Встроенные функции

Для операции округления в Python есть встроенные функции – и

round

– округляет число (number) до ndigits знаков после запятой. Это стандартная функция, которая для выполнения не требует подключения модуля math.

По умолчанию операция проводится до нуля знаков – до ближайшего целого числа. Например:

Чтобы получить целый показатель, результат преобразовывают в .

Синтаксически функция вызывается двумя способами.

1. – это округление числа до целого, которое расположено ближе всего. Если дробная часть равна 0,5, то округляют до ближайшего четного значения.
2. – данные округляют до знаков после точки. Если округление проходит до сотых, то равен «2», если до тысячных – «3» и т.д.

int

– встроенная функция, не требующая подключения дополнительных модулей. Её функция – преобразование действительных значений к целому путем округления в сторону нуля. Например

Для положительных чисел функция аналогична функции , а для отрицательных – аналогично . Например:

Чтобы число по int преобразовать по математическим правилам, нужно выполнить следующие действия.

1. Если число положительное, добавить к нему 0,5.
2. Если число отрицательное, добавить -0,5.

Синтаксически преобразование оформляется так:

Фаза (аргумент)

Мы можем представить комплексное число как вектор, состоящий из двух компонентов на плоскости, состоящей из и осей. Следовательно, две составляющие вектора — это действительная и мнимая части.

Угол между вектором и действительной осью определяется как или комплексного числа.

Формально это определяется как:

фаза (число) = arctan (мнимая_часть / действительная_часть)

где функция arctan является обратной математической функцией tan.

В Python мы можем получить фазу комплексного числа, используя модуль для комплексных чисел. Мы также можем использовать функцию и получить фазу из ее математического определения.

import cmath
import math

num = 4 + 3j

# Using cmath module
p = cmath.phase(num)
print('cmath Module:', p)

# Using math module
p = math.atan(num.imag/num.real)
print('Math Module:', p)

Вывод:

cmath Module: 0.6435011087932844
Math Module: 0.6435011087932844

Обратите внимание, что эта функция возвращает фазовый угол в , поэтому, если нам нужно преобразовать в , мы можем использовать другую библиотеку, например

import cmath
import numpy as np

num = 4 + 3j

# Using cmath module
p = cmath.phase(num)
print('cmath Module in Radians:', p)
print('Phase in Degrees:', np.degrees(p))

Вывод:

cmath Module in Radians: 0.6435011087932844
Phase in Degrees: 36.86989764584402

Важность функций

Абстракция

Человек бежит, машина едет, корабль плывёт, а самолёт летит. Всё это – объекты реального мира, которые выполняют однотипные действия. В данном случае, они перемещаются во времени и пространстве. Мы можем абстрагироваться от их природы, и рассматривать эти объекты с точки зрения того, какое расстояние они преодолели, и сколько времени на это ушло.

Мы можем написать функцию, которая вычисляет скорость в каждом конкретном случае

Нам не важно, кто совершает движение: и для человека и для самолёта средняя скорость будет рассчитываться одинаково

Это простой пример и простая функция, но абстракции могут быть куда более сложными. И именно тогда раскрывается настоящая сила функций. Вместо того чтобы решать задачу для каждого конкретного случая, проще написать функцию, которая находит решение для целого ряда однотипных, в рамках применяемой абстракции, объектов. В случае сложных и длинных вычислений, это повлечёт за собой значительное сокращение объёмов кода, а значит и времени на его написание.

Возможность повторного использования

Функции были созданы ради возможности их многократного применения. Код без функций превратился бы в огромное нечитаемое полотно, на порядки превышающее по длине аналогичную программу с их использованием.

Например, при работе с массивами чисел, вам нужно часто их сортировать. Вместо того чтобы реализовать простой алгоритм сортировки (или использовать встроенную функцию), вам пришлось бы каждый раз перепечатывать тело этой или похожей функции:

Всего 10 таких сортировок, и привет, лишние 60 строк кода.

Модульность

Разбитие больших и сложных процессов на простые составляющие – важная часть, как кодинга, так и реальной жизни. В повседневности мы занимаемся этим неосознанно. Когда убираемся в квартире, мы пылесосим, моем полы и окна, очищаем поверхности от пыли и наводим блеск на всё блестящее. Всё это – составляющие одного большого процесса под названием «уборка», но каждую из них также можно разбить на более простые подпроцессы.

В программировании модульность строится на использовании функций. Для каждой подзадачи – своя функция. Такая компоновка в разы улучшает читабельность кода и уменьшает сложность его дальнейшей поддержки.

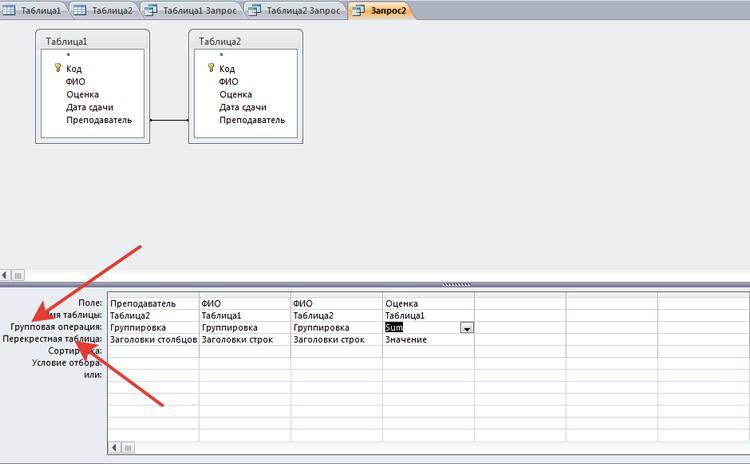
Допустим, мы работаем с базой данных. Нам нужна программа, которая считывает значения из базы, обрабатывает их, выводит результат на экран, а затем записывает его обратно в базу.

Без применения модульности получится сплошная последовательность инструкций:

Но если вынести каждую операцию в отдельную функцию, то текст главной программы получится маленьким и аккуратным.

Это и называется модульностью.

Пространство имен

Концепция пространства имён расширяет понятие модульности. Однако цель – не облегчить читаемость, а избежать конфликтов в названиях переменных.

Пример из жизни: в ВУЗе учатся два человека с совпадающими ФИО. Их нужно как-то различать. Если сделать пространствами имён группы этих студентов, то проблема будет решена. В рамках своей группы ФИО этих студентов будут уникальными.

Стандартные модули

Python распространяется с библиотекой стандартных модулей. Библиотека включает в себя более 200 модулей, которые выполняют платформенно-зависимую поддержку таких задач, как: интерфейс к операционной системе, управление объектами, поиск, сеть + интернет, GUI и т.д. Полный список стандартных модулей можно посмотреть на http://docs.python.org/library/.

Часть модулей встроена в интерпретатор по умолчанию, обеспечивая доступ к операциям; они встроены либо из соображений эффективности, либо для обеспечения доступа к примитивам операционной системы — например, модуль sys.

Переменная sys.path содержит список строк с именами каталогов, в которых происходит поиск модулей. Она инициализируется из значения переменной окружения PYTHONPATH и встроенного значения по умолчанию. Можно добавить путь:

>>> import sys
>>> sys.path.append(/home/my/lib/python)

Для выяснения имен, определенных в модуле, можно использовать встроенную функцию dir(). Она возвращает отсортированный список строк:

>>> dir(sys)

Что такое модуль

Python позволяет поместить классы, функции или данные в отдельный файл и использовать их в других программах. Такой файл называется модулем. Объекты из модуля могут быть импортированы в другие модули. Имя файла образуется путем добавления к имени модуля расширения .py. При импорте модуля интерпретатор ищет файл с именем my_module.py сначала в текущем каталоге, затем в каталогах, указанных в переменной окружения PYTHONPATH, затем в зависящих от платформы путях по умолчанию, а также в специальных файлах с расширением ‘.pth’, которые лежат в стандартных каталогах. Программист может внести изменения в PYTHONPATH и в ‘.pth’, добавив туда свой путь. Каталоги, в которых осуществляется поиск, можно посмотреть в переменной sys.path.

Большие программы, как правило, состоят из стартового файла — файла верхнего уровня, и набора файлов-модулей. Главный файл занимается контролем программы. В то же время модуль — это не только физический файл. Модуль представляет собой коллекцию компонентов. В этом смысле модуль — это пространство имен, — namespace, и все имена внутри модуля еще называются атрибутами — такими, например, как функции и переменные.

cmath vs math

A complex number is a combination of a real number and an imaginary number. It has the formula of a + bi, where a is the real number and bi is the imaginary number. Real and imaginary numbers can be explained as follows:

• A real number is literally any number you can think of.
• An imaginary number is a number that gives a negative result when squared.

A real number can be any number. For example, 12, 4.3, -19.0 are all real numbers. Imaginary numbers are shown as i. The following image shows an example of a complex number:

In the example above, 7 is the real number and 3i is the imaginary number. Complex numbers are mostly used in geometry, calculus, scientific calculations, and especially in electronics.

The functions of the Python module aren’t equipped to handle complex numbers. However, Python provides a different module that can specifically deal with complex numbers, the module. The Python module is complemented by the module, which implements many of the same functions but for complex numbers.

You can import the module as follows:

>>>

Since the module is also packaged with Python, you can import it the same way you imported the module. Before you work with the module, you have to know how to define a complex number. You can define a complex number as follows:

>>>

As you can see, you can determine that a number is indeed complex by using .

Note: In mathematics, the imaginary unit is usually denoted i. In some fields, it’s more customary to use j for the same thing. In Python, you use to denote imaginary numbers.

Python also provides a special built-in function called that lets you create complex numbers. You can use as follows:

>>>

You can use either method to create complex numbers. You can also use the module to calculate mathematical functions for complex numbers as follows:

>>>

Пакеты

Пакеты — способ структурирования пространств имен модулей на основе файловой системы. Пакетная организация дает все удобства по управлению большим количеством файлов. Пакетный импорт делает код более читабельным и значительно упрощает поиск. Если весь код структурирован в одном рутовом каталоге, все, что нужно добавить в PYTHONPATH — это рутовый каталог.

Так же, как применение модулей делает безопасным использование глобального пространства имен авторами различных модулей, применение пакетов делает безопасным использование имен модулей авторами многомодульных пакетов.

Например, есть пакет, который лежит в корневой папке TCP. В нем лежат два подкаталога — Server и Client:

TCP/
   _init_.py
   main.py
   
   Server/
         _init_.py
         tcp.py
         server.py
         lib.py
   Client/
         _init_.py
         tcp.py
         client.py
         lib.py

Файл _init_.py необходим для того, чтобы интерпретатор распознал каталог, как содержащий пакет. Обычно это пустой файл. Тогда импорт индивидуальных модулей пакета может быть таким:

>>> import TCP.Server.lib
>>> import TCP.Client.lib

Ссылка на функцию должна быть полной:

>>> import TCP.Server.lib.connect()

Можно сделать альтернативную загрузку:

>>> from TCP.Server import lib as server_lib 
>>> from TCP.Client import lib as client_lib 
>>> server_lib.connect()
>>> client_lib.connect()

Здесь вместо lib может быть подставлен модуль, подпакет или имя, определенное в TCP.Server — т.е. это может быть функция, класс или переменная.

Что касается варианта с импортом:

>>> from TCP import *

то в корневом __init__.py может быть определен список __all__ , в котором перечисляются модули, которые импортируются в этом случае. Например:

    __all__ = 

Импорт всех имен может привести к конфликтам. При этом глобальные переменные становятся доступными только на чтение — вместо них будут созданы локальные.

Math Methods

Method	Description
math.acos()	Returns the arc cosine of a number
math.acosh()	Returns the inverse hyperbolic cosine of a number
math.asin()	Returns the arc sine of a number
math.asinh()	Returns the inverse hyperbolic sine of a number
math.atan()	Returns the arc tangent of a number in radians
math.atan2()	Returns the arc tangent of y/x in radians
math.atanh()	Returns the inverse hyperbolic tangent of a number
math.ceil()	Rounds a number up to the nearest integer
math.comb()	Returns the number of ways to choose k items from n items without repetition and order
math.copysign()	Returns a float consisting of the value of the first parameter and the sign of the second parameter
math.cos()	Returns the cosine of a number
math.cosh()	Returns the hyperbolic cosine of a number
math.degrees()	Converts an angle from radians to degrees
math.dist()	Returns the Euclidean distance between two points (p and q), where p and q are the coordinates of that point
math.erf()	Returns the error function of a number
math.erfc()	Returns the complementary error function of a number
math.exp()	Returns E raised to the power of x
math.expm1()	Returns Ex — 1
math.fabs()	Returns the absolute value of a number
math.factorial()	Returns the factorial of a number
math.floor()	Rounds a number down to the nearest integer
math.fmod()	Returns the remainder of x/y
math.frexp()	Returns the mantissa and the exponent, of a specified number
math.fsum()	Returns the sum of all items in any iterable (tuples, arrays, lists, etc.)
math.gamma()	Returns the gamma function at x
math.gcd()	Returns the greatest common divisor of two integers
math.hypot()	Returns the Euclidean norm
math.isclose()	Checks whether two values are close to each other, or not
math.isfinite()	Checks whether a number is finite or not
math.isinf()	Checks whether a number is infinite or not
math.isnan()	Checks whether a value is NaN (not a number) or not
math.isqrt()	Rounds a square root number downwards to the nearest integer
math.ldexp()	Returns the inverse of math.frexp() which is x * (2**i) of the given numbers x and i
math.lgamma()	Returns the log gamma value of x
math.log()	Returns the natural logarithm of a number, or the logarithm of number to base
math.log10()	Returns the base-10 logarithm of x
math.log1p()	Returns the natural logarithm of 1+x
math.log2()	Returns the base-2 logarithm of x
math.perm()	Returns the number of ways to choose k items from n items with order and without repetition
math.pow()	Returns the value of x to the power of y
math.prod()	Returns the product of all the elements in an iterable
math.radians()	Converts a degree value into radians
math.remainder()	Returns the closest value that can make numerator completely divisible by the denominator
math.sin()	Returns the sine of a number
math.sinh()	Returns the hyperbolic sine of a number
math.sqrt()	Returns the square root of a number
math.tan()	Returns the tangent of a number
math.tanh()	Returns the hyperbolic tangent of a number
math.trunc()	Returns the truncated integer parts of a number

Арифметические операции

Подобно действительным числам, комплексные числа также можно складывать, вычитать, умножать и делить. Давайте посмотрим, как мы могли бы это сделать в Python.

a = 1 + 2j
b = 2 + 4j
print('Addition =', a + b)
print('Subtraction =', a - b)
print('Multiplication =', a * b)
print('Division =', a / b)

Выход:

Addition = (3+6j)
Subtraction = (-1-2j)
Multiplication = (-6+8j)
Division = (2+0j)

ПРИМЕЧАНИЕ. В отличие от действительных чисел, мы не можем сравнивать два комплексных числа. Мы можем сравнивать только их действительную и мнимую части по отдельности, поскольку это действительные числа. Приведенный ниже фрагмент доказывает это.

>>> a
(4+3j)
>>> b
(4+6j)
>>> a < b
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: '<' not supported between instances of 'complex' and 'complex'

Операции над числами

Манипуляции над числовыми значениями в языке программирования Python выполняются благодаря множеству различных операций, символьные обозначения которых, как правило, совпадают с аналогами из традиционной математики. Таким образом, можно прибавлять, отнимать, умножать, делить, находить остаток от деления и возводить в степень числовые значения любых разновидностей. Ознакомиться с основными типами операций, которые выполняются над цифровыми значениями, можно из следующей небольшой таблицы:

Операция	Назначение
a + b	Сложение a и b
a – b	Разница между a и b
a * b	Умножение a на b
a / b	Деление a на b
a % b	Остаток от деления a на b
a // b	Целая часть от деления a и b
a ** b	Возведение a в степень b

Помимо вышеперечисленных арифметических действий, над числами можно осуществлять битовые операции, которые задействуют их двоичное представление. Перечень подобных операций представлен в следующей таблице, где можно найти назначение каждой из них:

Операция	Назначение
a & b	Побитовое И для a и b
a | b	Побитовое ИЛИ для a и b
a ^ b	Исключающее ИЛИ для a и b
~a	Инверсия битов для a
a << b	Побитовый сдвиг влево для a на b
a >> b	Побитовый сдвиг вправо для a на b

Также для более эффективной обработки числовых данных в Python были добавлены особые методы, позволяющие всего за одно действие осуществлять множество сложных операций. К наиболее популярным из них относятся методы, предназначенные для быстрого нахождения квадратного корня, модуля, а также округления числа. Чтобы воспользоваться некоторыми арифметическими функциями, необходимо подключить стандартную библиотеку math при помощи вызова . Список популярных методов представлен в данной таблице:

Метод	Назначение
sqrt(a)	Квадратный корень из a
log(a)	Натуральный логарифм из a
fabs(a)	Возвращает модуль a
round(a)	Округляет a до ближайшего целого
round(a, b)	Округляет a до b знаков после точки
floor(a)	Округляет a до меньшего целого значения
ceil(a)	Округляет a до большего целого значения
isfinite(a)	Проверяет, является ли a числом
modf(a)	Возвращает целую и дробную части a
sin(a)	Синус угла a, указанного в радианах
cos(a)	Косинус угла a, указанного в радианах
tan(a)	Тангенс угла a, указанного в радианах

Функция fabs модуля math вначале пытается привести аргумент к вещественному типу (float), и только потом вычисляет модуль. Для вычисления модуля числа так же есть стандартная функция abs.

Ввод числа с клавиатуры

Для того чтобы получить числовые данные от пользователя используется стандартный метод input. Его вызов позволяет получать ввод информации с клавиатуры, который выполняется во время запуска программы на компьютере. В качестве аргумента для этого метода можно использовать строку, предлагающую пользователю ввести числовые сведения. Ниже показан пример того, как ввести в Pyhon с клавиатуры число. Переменная n получает значение и отображается на экране с помощью print:

n = input("Press n: ")
print("n = " + str(n))

Press n: 10
n = 10

Максимальное значение

Получить максимальное значение целочисленной переменной, которое поддерживается в текущей версии языка Python можно с помощью переменной sys.maxsize. Как правило, на разных компьютерах это число совпадать не будет из-за разной архитектуры процессоров. На данный момент из Python были убраны любые ограничения, касающиеся размерности вводимых величин. Вывести на экран максимальное число в Python можно следующим образом:

import sys
print(sys.maxsize)

9223372036854775807

Как сделать и вставить гиперссылку на слайд в презентации — примеры оформления

Для повторения значения

Предположим, вы хотите повторить определенное значение, вы можете создать итератор для повторяющегося значения, используя .

Например, если вы хотите построить последовательность вида , где i находится в диапазоне от 0 до 10, вы можете использовать эту функцию.

import itertools

data = list(zip(range(10), itertools.repeat(5)))
print(data)

Выход

Действительно, нам удалось легко сделать эту последовательность.

Другой пример, в котором эта функция полезна, — если вы пытаетесь построить квадраты с помощью map() в Python.

squares = list(map(pow, range(10), itertools.repeat(2)))
print(squares)

Выход

Видите, как легко мы смогли построить его с помощью .