Как посчитать проценты: от числа, от суммы чисел и др. [в уме, на калькуляторе и с помощью excel]

Пропорция

Нередки случаи, когда необходимо решить задачи на проценты, используя пропорцию. На самом деле этот метод нахождения результата в значительной мере облегчает задачу учащимся, преподавателям и не только.

Итак, что такое пропорция? Под этим термином понимается равенство двух отношений, которые можно выразить следующим образом: А/_В = С/_D.

В учебниках математики значится такое правило: произведение крайних членов равняется произведению средних. Это выражается следующей формулой: А х D = В х С.

Благодаря этой формулировке, можно вычислить любое число, если три других члена пропорции известны. К примеру, А – неизвестное число. Чтобы его найти, нужно

При решении задач методом пропорции необходимо понимать, от какого числа брать проценты. Бывают случаи, когда доли нужно взять от разных величин. Сравните:

1. После окончания распродажи в магазине стоимость футболки возросла на 25% и составила 200 рублей. Какова была стоимость во время распродажи.

Решение:

В данном случае нужно величина 200 рублей соответствует 125% от первоначальной (распродажной) цены футболки. Тогда, чтобы узнать ее стоимость во время распродажи, нужно (200 х 100) : 125. Получится 160 рублей.

2. На планете Виценция 200 000 жителей: люди и представители гуманоидной расы Наави. Наави составляют 80% от всего населения Виценции. Из людей 40% заняты обслуживанием рудника, остальные добывают тетаниум. Сколько людей добывают тетаниум?

Решение:

В первую очередь нужно найти в численном виде количество людей и количество Наави. Так, 80% от 200 000 будет равняться 160 000. Столько представителей гуманоидной расы проживает на Виценции. Количество людей, соответственно, равняется 40 000. Из них 40%, то есть 16 000, обслуживают рудник. Значит, 24 000 людей занимаются добычей тетаниума.

Эффективная процентная ставка по вкладу

Эта характеристика актуальна только для вкладов с капитализацией процентов. В связи с тем, что проценты не выплачиваются а идут на увеличение суммы вклада, очевидно, что если ежемесячно возрастает сумма вклада, то и вновь начисленные на эту сумму проценты также будут выше, как и конечный доход.

Если рассчитать, сколько процентов было начислено к начальной сумме к концу срока вклада, эта величина и будет являться эффективной процентной ставкой.

Формула расчета эффективной ставки:

где N — количество выплат процентов в течение срока вклада,T —  срок размещения вклада в месяцах.

Эта формула не универсальна. Она подходит только для вкладов с капитализацией 1 раз в месяц, период которых содержит целое количество месяцев. Для других вкладов (например вклад на 100 дней) эта формула работать не будет.

Однако есть и универсальная формула для рассчета эффективной ставки. Минус этой формулы в том, что получить результат можно только после рассчета процентов по вкладу.

Эта формула подходит для всех вкладов, с любыми сроками и любой периодичностью капитализации. Она просто считает отношение полученного дохода к начальной сумме вклада, приводя эту величину к годовым процентам. Лишь небольшая погрешность может присутствовать здесь, если период вклада или его часть выпала на високосный год.

Именно этот метод используется для рассчета эффективной ставки в представленном здесь депозитном калькуляторе.

Математическое объяснение

С точки зрения математики и ее основ решение задачи о том, как рассчитать процент от суммы, сводится только к применению простейших правил раскрытия скобок при умножении суммы на единое число и поиска общего знаменателя, который, в общем-то, им и является. Другими словами, представить в формульном выражении это можно так:

a x (b + c) = ab + ac ,

где ab и ac – произведения слагаемых в скобках (b и c) на число (коэффициент) перед скобками a.

Собственно, в пропорции действует тот же метод. Допустим, у нас есть некое число z, представляющее собой 100%, и сумма чисел a и b. Процент, который нужно вычислить, обозначим неизвестным числом y. В таком варианте пропорция принимает вид:

Отсюда простое решение:

((a + b) x 100%)/z = ((a x 100%) + (b x 100%))/z

В скобки действия взяты для того, чтобы подчеркнуть, что операции умножения выполняется в первую очередь, а сложение произведений – во вторую. Такое же действие производится, если изначально сумма чисел составляет 100%.

Примеры школьных заданий

Из запланированной дистанции в 32 км Том пробежал только 76%. Сколько километров пробежал мальчик?
Решение: для вычислений подходит первый калькулятор. В первую ячейку вставляем 76, во вторую — 32.
Получаем: Том пробежал 24.32 км.

Фермер Купер собрал с поля 500 кг кукурузы. 160 кг из этой массы оказалось неспелой. Сколько процентов от общего числа составила неспелая кукуруза?
Решение: для расчёта подходит второй калькулятор. В первое окошко записываем число 160, во второе — 500.
Получаем: 32% кукурузы оказалось неспелой.

Майкл прочитал своей подруге на ночь 112 страниц, что составляет 32% всей книги. Сколько страниц в книге?
Решение: используем для расчёта третий калькулятор. Вставляем в первую ячейку значение 112, а во вторую — 32.
Получаем: в книге 350 страниц.

Длина маршрута, по которому ходил автобус №42, составляла 48 километров. После добавления трёх дополнительных остановок расстояние от начальной до конечной станции изменилось до 78 километров. На сколько процентов изменилась длина маршрута?
Решение: используем для вычисления четвёртый калькулятор. В первую ячейку вбиваем число 78, во вторую — 48.
Получаем: длина маршрута выросла на 62.5%.

Братство металла и макулатуры в мае сдало на лом 320 кг цветного металла, а в июне на 30% больше. Сколько металла сдали ребята из братства в июне?
Решение: для расчёта будем использовать пятый калькулятор. В первую ячейку вставляем число 30, а во второе число 320.
Получаем: в июне братство сдало 416 кг металла.

Энди прорыл во вторник 3 метра туннеля, а в среду в связи с отъездом друга в Ирландию — на 22% меньше. Сколько метров туннеля прорыл Энди в среду?
Решение: в данном случае подходит шестой калькулятор. В первую ячейку вставляем 22, во вторую — 3.
Получаем: в среду мальчик прорыл 2.34 метра туннеля.

Считаем процент от суммы вклада

Напомню, что проценты по банковскому вкладу могут быть простыми и сложными.

В первом случае банк начисляет доход на начальную сумму депозита. То есть, каждый месяц/квартал/год вкладчик получает от банка один и тот же «бонус».

Схема со сложными процентами для вкладчика выгоднее. Начисленный за месяц доход «плюсуется» к сумме вклада. И уже в следующем периоде процент будет насчитываться на большую сумму. А в следующем – на еще большую и так далее. На «длинных» сроках (10-20 лет) сложные проценты творят настоящие чудеса!

Конечно, формулы расчета для простых и сложных процентов отличаются друг от друга.

Рассмотрим их на конкретном примере.

Доходность по вкладу с простыми процентами

Сумма % = (вклад*ставка*дней в расчетном периоде)/(дней в году*100)

Пример. Валера открыл вклад на сумму 20 000 рублей под 9% годовых на один год.

Рассчитаем доходность вклада за год, месяц, неделю и один день.

Сумма процентов за год = (20 000*9*365)/(365*100) = 1800 рублей

Понятно, что в нашем примере годовую доходность можно было посчитать гораздо проще: 20 000*0,09. И в результате получить те же самые 1800 рублей. Но раз решили считать по формуле, то и будем считать по ней. Главное – понять логику.

Сумма процентов за месяц (июнь) = (20 000*9*30)/(365*100) = 148 рублей

Сумма процентов за неделю = (20 000*9*7)/(365*100) = 34,5 рублей

Сумма процентов за день = (20 000*9*1)/(365*100) = 5 рублей

Согласитесь, формула простых процентов элементарна. Она позволяет рассчитать доходность по вкладу за любое количество дней.

Доходность по вкладу со сложными процентами

Усложняем пример. Формула расчета сложных процентов уж чуть «мудреней», чем в предыдущем варианте. Калькулятор должен иметь функцию «степень». Как вариант, можно использовать опцию степень в таблице Excel.

• Сумма % = вклад*(1+ ставка за период капитализации)число капитализаций — вклад
• Ставка за период капитализации = (годовая ставка*дни в периоде капитализации)/(число дней в году*100)

Вернемся к нашему примеру. Валера разместил на банковском вкладе те же 20 000 рублей под 9% годовых. Но в этот раз — с ежемесячной капитализацией процентов.

Сначала посчитаем ставку за период капитализации. По условиям вклада проценты начисляются и «плюсуются» к депозиту один раз в месяц. Значит, в периоде капитализации у нас 30 дней.

Таким образом, ставка за период капитализации = (9*30)/(365*100) = 0,0074%

А теперь считаем, сколько наш вклад принесет в виде процентов за разные периоды.

Сумма процентов за год = 20 000*(1+0,0074) 12 – 20 000 = 1 850 рублей

В степень «12» мы возводим, потому что год включает двенадцать периодов капитализации.

Как видите, даже на такой символической сумме и коротком сроке разница в доходности вклада с простыми и сложными процентами составляет 50 рублей.

Сумма процентов за полгода = 20 000*(1+0,0074) 6 – 20 000 = 905 рублей

Сумма процентов за квартал = 20 000*(1+0,0074) 3 – 20 000 = 447 рублей

Сумма процентов за месяц = 20 000*(1+0,0074) 1 – 20 000 = 148 рублей

Вкладчик получит все те же 148 рублей и с простыми, и со сложными процентами. Расхождения в доходности начнутся со второго месяца. И чем длиннее срок депозита – тем существенней будет разница.

Пока мы не отошли далеко от темы сложных процентов, давайте проверим, насколько справедлива одна из рекомендаций финансовых консультантов. Я имею в виду совет выбирать вклады с капитализацией процентов не раз в полгода или квартал, а раз в месяц.

Предположим, наш условный Валера оформил депозит на ту же сумму, срок и под ту же ставку, но с капитализацией процентов раз в полгода.

Для начала нам придется пересчитать ставку за период капитализации. Ведь теперь этот период составляет не 30 дней (месяц), а 182 дня (полгода).

Ставка = (9*182)/(365*100) = 0,0449%

Теперь считаем доходность по вкладу за год.

Сумма процентов за год = 20 000*(1+0,0449) 2 – 20 000 = 1 836 рублей

Вывод: при прочих равных условиях полугодовая капитализация принесет Валере на 14 рублей меньше, чем ежемесячная (1850 – 1836).

Понимаю, что разница совсем невелика. Но ведь и другие исходные данные у нас символические. На крупных суммах и длинных сроках 14 рублей превратятся в тысячи и миллионы.

Расчёт суммы процентов по кредиту с помощью кредитного калькулятора онлайн

В любом из возможных случаев, мы рекомендуем пользоваться кредитным калькулятором онлайн. Это полностью убирает человеческий фактор, возможность сотрудника банка злоупотребить Вашим доверием и просто облегчает расчёты кредита.

К фиксированным мы относим процентную ставку. Да, некоторые банки предоставляют возможность использования изменяемой кредитной ставки, но об этом мы говорили в другой статье. К не фиксированным процентам мы относим комиссии: “за досрочное погашение кредита”, “за выдачу наличных”, “за просроченный платёж по кредиту” и другие. Воспользуйтесь блоком досрочное погашение, если Вы уже совершали его. Добавьте ежемесячные и единоразовые комиссии, это позволит рассчитать всю сумму процентов по кредиту.

Нажмите кнопку “Рассчитать” и Вы получите полный график платежей, включая процентную ставку, указанные ранее комиссии и досрочные погашения кредита

Обратите внимание на блок “Общие данные”, в нём есть колонка “Начисленные проценты” – это и будет сумма процентов по кредиту. Если Вы хотите более детально рассмотреть в какой из месяцев и сколько заплатите процентов по кредиту, нажмите на кнопку “Загрузить ещё … количество строк”

Распечатайте на принтере, сохраните или отправьте по электронной почте график платежей. Это позволит сравнить полученный график с графиком представленным банком. Так Вы легко поймете о скрытых комиссиях и возможных переплатах, о которых банк умолчал ранее.

Как посчитать, сколько это процентов?

Этот вопрос задает каждый покупатель магазина, который намеревается воспользоваться акцией, и каждый сотрудник компании, желающий узнать размер своего вознаграждения за выполнение плана. Ведь проценты присутствуют во многих сферах повседневной жизни.

Возьмем конкретный пример. В магазине наушники стоили 3000 рублей, на них появилась акция в виде скидки 30%. Какая сумма вашей выгоды и сколько надо заплатить за товар?

Расчет простой

• 3000×30/100 = 900, поскольку 30/100 можно еще записать как 0,30, то
• 3000×0,30 = 900 рублей — это сумма скидки (30%) в денежном эквиваленте.

Теперь посчитаем сколько надо заплатить за наушники: 3000-900=2100 руб.

Расчет процентов — это не только задание на уроке в школе, но и актуальный вопрос для многих взрослых. Не у всех есть способность быстро выполнять действия в уме. Хотя рассчитать 10% или 20% от заданной суммы довольно просто, вычисление размера, например процентной ставки по банковским операциям иногда бывает проблематичным.

Что делать в этой ситуации? Вы можете прибегнуть к помощи специалиста, но проще применить свои навыки в использовании современных технологий и использовать онлайн калькулятор расчета процентов.

О легких и простых методах расчета процентов вы узнаете из видео.

Читайте далее:

Калькулятор автокредита: рассчитать процент переплаты

Онлайн конвертер долей, перевод дюжин, процентов, промилле и других единиц

Особенности ипотечного кредита: что нужно знать перед оформлением

Калькулятор сравнения шин, преимущества и недостатки изменения размера

Калькулятор расхода топлива, как рассчитать стоимость поездки

Как рассчитать доходность сделок по акциям, калькулятор расчета

Расчет при помощи онлайн-калькулятора

Вычислить процент при помощи обычного онлайн-калькулятора не представляет труда.

Многие из них сделаны по принципу стандартных устройств, а потому вычисления проходят по выше указанной схеме.

Если же на онлайн-калькуляторе нет кнопки «%», вычисления могут проходить двумя способами:

1. Необходимо разделить процент на 100 и умножить на данное число. Пример: выделить 15% от 300. 15/100 = 0,15; 0,15*300 = 45.
2. Разделить число на 100 и умножить на процент: 300/100 = 3; 3*15 = 45.

Если нахождение необходимо для оплаты кредита, ипотеки, ОСАГО или налоговых вычетов, можно воспользоваться специализированными калькуляторами. Их легко найти по поиску.

Они значительно отличаются от простых калькуляторов: например, при расчете стоимости ОСАГО потребуется выбрать тип автомобиля, мощность двигателя, указать стаж, возраст и область и некоторые другие данные. Исходя из этих данных, калькулятор сосчитает примерную среднюю стоимость в рублях полиса.

Стоит отметить: к сожалению, полученная при таких подсчетах сумма лишь примерна – правильные данные будут рассчитаны специалистом при личном обращении.

Статьи о кредитах

Как на калькуляторе посчитать проценты

Лайфхак для подсчета процентов

Британец Бен Стефенс поделился в своем Twitter простым математическим трюком, существенно упрощающим подсчет процентов без калькулятора. Его можно сформулировать так: «А процентов от В — это то же самое, что В процентов от А».

Вроде бы ничего особенного, но в некоторых случаях помогает и еще как. Например, попробуй быстро посчитать сколько будет 16 % от 25. А 25 % от 16? И в том, и в другом случае ответ 4, но справиться со вторым примером, согласись, куда проще.

«Имею диплом математика и никогда об этом не задумывался», — пишут под твитом Бена одни пользователи. «Попробуй так найти 63 % от 11», — ехидничают другие. Что же, способ Бена действительно лучше работает с числами кратными 0 или 5. А 63 % от 11 будем находить по старинке.

Как вычислить процент от числа

Первый способ. Умножь процент и число друг на друга, а затем раздели на 100.
63 % от 11
63х11/100 = 693/100 = 6,93

Второй способ. Раздели число на 100 и умножь на процент.
63 % от 11
11/100 = 0,11 0,11х63 = 6,93

Кстати, легко умножать в уме любые двузначные числа на 11 мы научились в статье о приемах устного счета.

А если вместо 63 % от 11 найти 11 % от 63? На мой взгляд, лайфхак Бена вполне применим и здесь.
63 % от 11 — это то же, что и 11 % от 63
11 % = (10+1) %
63/10 = 6,3
63/100 = 0,63
6,3+0,63 = 6,93

Как узнать процент скидки

Пачка стирального порошка стоила в магазине 400 рублей. Сегодня в магазине скидки и на ценнике стоит 372 рубля. Как определить размер скидки в процентах?

Тут нужно составить пропорцию. Примем цену без скидки за 100 %, а цену со скидкой за х %. Тогда будет справедливым следующее равенство:
400/372 = 100/х
отсюда х = 372х100/400 = 93 %
Соответственно скидка составляет 7 %.

Узнаем процент с помощью калькулятора

Чтобы узнать процент от числа, введи число, знак умножения, затем нужный процент и знак %. Для задачи с порошком 7 % от 400 находим так: 400 × 7 %

Если нужно узнать цену после скидки, набери на калькуляторе: 400 — 7 %.

Небольшая подсказка: чтобы долго не искать калькулятор в меню смартфона, воспользуйся адресной строкой браузера (подойдет как «Яндекс», так и Google).

Как вычислить сложный процент с помощью онлайн-сервиса

Не все проценты можно посчитать, даже вооружившись нашей инструкцией.

Проценты по вкладам, доходность инвестиций, переплата по ипотеке — всё это проще вычислить, воспользовавшись удобными онлайн-сервисами.

Так, кредитный калькулятор в одно нажатие кнопки позволит рассчитать стоимость кредита, ежемесячные платежи погашения займа, полную сумму переплаты. А калькулятор сложных процентов поможет с начислением сложных процентов в банковском депозите (когда по окончании каждого периода начисленные проценты становятся основной суммой).

Яркие ценники, сигнализирующие о скидках, способны привлечь каждого. Но нужно быть бдительным. Ведь за пестрой россыпью процентов со знаком минус ушлые маркетологи иногда умудряются сбыть нам товар даже по более высоким ценам, чем до распродажи. А не попасться в их ловушки, сохранить деньги и сделать жизнь чуточку проще тебе, надеюсь, позволят наши полезные советы.

Быстрое вычисление процентов

Конечно, вычисление процентов при помощи пропорции является фундаментальным. Однако с применением дробных чисел это процедура упрощается до невозможности. Ведь что такое 50% на самом деле? Половина. То есть 1/2 или 0,5 (исходя из начального числа 1). Теперь понятно: чтобы вычислить половину, нужно умножить искомое число или на 1/2, или на 0,5 либо разделить на 2. Такой способ, правда, годится только для чисел, которые делятся без остатка.

В случае возникновения остатка или бесконечных знаков в периоде после запятой типа 0,33333333… лучше использовать дробные выражения наподобие 1/3. Кстати, именно дроби (в некоторых случаях иррациональные) со всей точностью отражают само число, ведь периодические цифры после запятой, сколько ни задавай, все равно целого числа не дадут. А так та же одна треть четко и понятно выражает саму суть.

В тех же рецептах, естественно, треть можно определить, так сказать, на глаз. А вот в химических процессах, особенно связанных с тонкой дозировкой компонентов, скажем, в фармацевтике, такой метод не подойдет. Здесь на глаз полагаться не приходится. Необходимо использовать точные соотношения ингредиентов, даже если один из показателей имеет вид числа с цифрой в периоде или представлен в виде той же иррациональной дроби. Но, как правило, к примеру при взвешивании, такие числа могут ограничиваться после запятой десятитысячными или максимум стотысячными.

Насколько число меньше другого в процентах

К примеру: обычная стоимость порошка – 500 рублей. По акции, цену снизили до 480 рублей. Насколько цена по акции, меньше первоначальной в процентах? Вначале находят процентную составляющую акционной цены от базовой, а затем находиться их разница. Составляем пропорцию:

Вычисляем по формуле: (480*100)/500=96. 100%-96%=4%. Цена по акции меньше первоначальной на 4%.

Насколько число больше другого в процентах. Пример: клавиатура стоила 300 рублей, а после повышения курса доллара, цена выросла до 390 рублей. Насколько изменилась цена на клавиатуру в процентах? Вначале находиться общая процентная ставка новой цены, относительно первоначальной, затем вычисляется их разница. Составляем пропорцию:

Вычисляем по формуле: (390*100)/300=130. 130%-100%=30%. Цена выросла на 30%.

Неизвестное число больше известного на определенный процент. Пример: товар в магазине, дороже товара на складе на 15%.  Цена сахара на складе – 50 рублей и приравнивается к 100%. Магазинная цена  – 100%+15%=115%. Вычисляем по формуле: (115*50)/100=57,5

Неизвестное число меньше известного на заданный процент. Пример: оптом на 5% дешевле. Цена за розницу – 60 рублей и равна 100 процентам, за опт – 100%-5%=95%. Составляем пропорцию:

Вычисляем по формуле: (60*95)/100=57

Процент между двумя числами. Ситуация, когда известно число, составляющее 100% и число, составляющее некую долю от первоначального. Пример: ожидалась партия в 60 коробок, а завезли 53. На сколько процентов выполнился план. Составляем пропорцию:

Вычисляем по формуле: (53*100)/60=88,3

Самая сложная «задача» — не запутаться в составлении пропорции.

Что такое проценты?

Это слово произошло от английского словосочетания Pro Centum

Прочитав это словосочетание, вы наверняка обратили внимание, что там присутствует слово цент. От этого и происходит смысл процентов

Как известно, цент — одна сотая часть от доллара. Поэтому 1% — это и есть одна сотая часть от числа.

Сейчас в процентах измеряются многие финансовые показатели:

1. налоги,
2. доли в бизнесе,
3. доходность от инвестиций,
4. премии и штрафы,
5. инфляция.

И не только финансовые:

1. рождаемость и смертность,
2. статистика удачных и неудачных браков,
3. коэффициент полезного действия.

Давайте разберёмся более подробно, как посчитать процент от суммы. Мы приведём вам несколько примеров, которые помогут вам все понять.

Пример 1. Водитель таксомоторной службы отработал смену. За день его выручка составила 5 тыс. рублей. Ему необходимо отдать службе такси комиссию с этих заказов — 15%. Чтобы узнать сумму, которую должен заплатить водитель, необходимо 5 тыс. умножить на 15, после чего разделить на 100. Мы получаем результат, равный 750 рублей. Как вы уже догадались, 15% — это 15 частей из ста.

Теперь мы приведём вам обратный пример с тем же водителем такси. Так, за смену он заработал 5 тыс. рублей. Он потратил определённую часть этих денег на обязательные расходы:

1. комиссию службе такси — 750 рублей,
2. мойку автомобиля — 250 рублей,
3. топливо — 1 тыс. рублей.

Итого у водителя остаётся 3 тыс. рублей. Из заработанных 5 тыс. рублей себе он забирает только 3. Теперь наша задача посчитать, какую часть от общей выручки он может смело положить к себе в карман. Для этого нам нужно разделить 3 тыс. на 5 тыс. После чего полученный результат, равный 0,6, умножить на 100%. Получается, водитель забирает себе в карман 60% от общей выручки.

Это интересно: разрядные слагаемые что это?

Пример 2. Четыре акционера открыли бизнес. Спустя год упорной работы он начал приносить доходы. Партнёры решили делить прибыль поровну, то есть каждому достанется по 25% от прибыли. Нам нужно посчитать, сколько денег получит каждый из них.

Допустим, бизнес приносит доход 200 тысяч рублей в месяц. Чтобы посчитать прибыль каждого из акционеров, необходимо умножить 200 тыс. на 25, и разделить на 100. Получаем результат — 50 тыс. рублей.

Пример 3. Конверсия продаж. Менеджер по продажам предлагает услуги своей компании по телефону. За месяц он совершил 800 звонков. Заинтересовались в услугах компании 280 клиентов. Для подсчёта конверсии продаж необходимо 280 разделить на 800, после чего умножить на 100. Результат будет равен 35%.

Сложные проценты по кредиту

В данном случае начисления сумма процентов за каждый расчетный период прибавляется к телу кредита. Общий размер долга растет, и вместе с ним увеличиваются и выплаты. Поэтому такая схема также называется «проценты на проценты». Банки применяют ее редко и, в основном, для долгосрочных займов.

Формула расчета сложных процентов выглядит следующим образом:

Сумма долга = Изначальная сумма × (1 + процентная ставка за расчетный период/100%)^число расчетных периодов

По ней можно посчитать переплату за один или за несколько расчетных периодов.

Пример:

Валерия Климова взяла 1 000 000 рублей на пять лет. Процентная ставка — 19% годовых, начисляется каждый месяц.

Вначале узнаем размер ежемесячной процентной ставки:

19%/12=1,58%

Как посчитать сложные проценты за первый месяц:

1 000 000(1+1,58%/100)^1=1 000 000(1+0,0158)=1 000 000 × 1,0158 = 1 015 800 рублей

Размер суммы долга за первые три месяца:

1 000 000(1+1,58%/100)^3=1 000 000(1+0,0158)^3=1 000 000 × 1,0158^3 = 1 000 000 × 1,0482 = 1 048 200 рублей

Размер долга за год:

1 000 000(1+1,58%/100)^12=1 000 000 × 1,0158^12 = 1 000 000 × 1,207 = 1 207 000 рублей

Размер долга за весь срок:

1 000 000(1+1,58%/100)^60=1 000 000 × 1,0158^60 = 1 000 000 × 2,5615 = 2 561 500 рублей

К концу срока Валерия должна будет вернуть на 1 561 500 рублей больше, чем взяла.

На этом примере видно, как увеличивается долг в течение срока.

Как считать проценты на калькуляторе: простейшие способы

Учитывая, что сегодня так называемые «счетные машинки» находятся на столе у любого школьника, продавца или бухгалтера, а также на любом телефоне и компьютере, нам не остается ничего другого, как считать проценты на калькуляторе. Мы не зря в начале статьи вспомнили школу и ваш дружный (а может и не дружный) шестой класс. Отбросив эти романтические переживания, перейдем к подсчету процентов.

Как вычислить процент от суммы: 1 способ

Давайте найдем необходимый процент с помощью простого примера. Допустим, вам необходимо найти 25% от суммы в 1000 рублей. Решаем следующий пример:

1000*25:100= 250

Как вычислить процент от суммы: 2 способ

Этот подсчет еще проще:

1000*0,25=250

Как вычислить процент от суммы: 3 способ

Ну и вычисление для совсем ленивых:

1000*25%=250

Вот вы и узнали простые способы, как посчитать проценты на калькуляторе. Мы уверены, что вы о них знали со школьной скамьи, и просто напомнили вам. Теперь вы можете применить эти знания и без проблем вычислить проценты по кредиту или по вкладу, самостоятельно подсчитав сумму процентов.

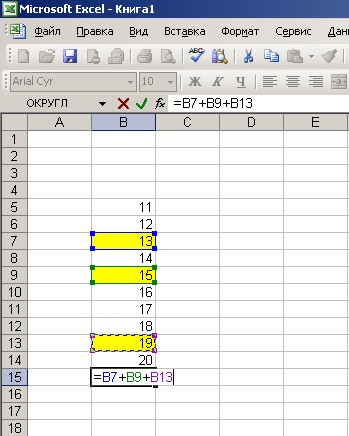
Как считать проценты в excel?

Если у вас под рукой имеется компьютер или ноутбук с операционной системой Windows, вам не составит большого труда подсчитать процент от необходимой суммы. Приведем для этого простой пример.

Нам необходимо найти 8% от 358.

1. Открываем Excel.
2. Находим свободную строку.
3. Вводим данные.
4. Ставим знак «=» и делаем подсчет.
5. Получаем 28,64.

Аналогично к подсчетам на калькуляторе, вы можете ввести в Excel знак %, и это тоже будет правильно.

Иногда нам необходимо узнать процентный показатель от суммы.

1. К примеру, у нас есть список сотрудников и сумма, на которую они произвели продаж. Помимо этого, известна сумма возвратов. По этим данным мы рассчитываем процент возвратов по товарам.
2. Просчитаем процент для первого показателя в списке — процент возвратов некоего Петрова.
3. Для начала составляем пропорцию, где 100% — это 35682(сумма продаж Петрова). х% — 2023 (сумма возвратов Петрова).
4. Решаем эту пропорцию по формуле, известной нам со школы.
5. Прописываем формулу в ячейке D2 и спускаемся немного вниз =C2*100%/B2.
6. К ячейке, в которой высветился результат, применяем формат «Процентный». Выделяем ячейки, правой кнопкой жмем на любой из них и выбираем «Формат». Во вкладке «Число» выбираем «Процентный». Система автоматически пропишет значок %.

7. Применив нашу формулу ко всем данным, получаем результат.

Видео: как посчитать проценты от суммы?