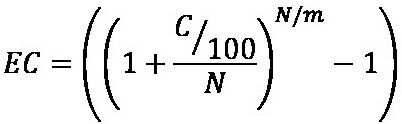Банковский вклад

Как искать процент от числа

Школьные задачи на сложные проценты

Например, возьмем задачи из учебника для 9 класса авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир «Аглгебра». (Номер в скобках)

Задача 1. (556) Костюм стоил 600 грн. После того как цена была снижена дважды, он стал стоить 432 грн., Причем процент снижения второй был в 2 раза больше, чем в первый раз. На сколько процентов каждый раз снижалась цена?

Решение: Для упрощения вычислений обозначим X – первая скидка; X/2 – вторая скидка. Для вычисления неизвестной X составляем уравнение Упрощаем, и сводим к квадратному уравнению и решаем Первый решение не имеет физического смысла, второй учитываем при вычислениях. Значение 0,2 соответствует снижению на 0,2*100%=20% после первой скидки, и X/2 =10% после второй скидки.

Задача 2. (557) Определенный товар стоил 200 грн. Сначала его цену повысили на несколько процентов, а затем снизили на столько же процентов, после чего стоимость его стала 192 грн. На сколько процентов каждый раз происходила смена цены товара?

Решение: Поскольку проценты одинаковы, то обозначаем изменении цены товара через X. На основе условия задачи получим уравнение Его упрощение приведет к решению уравнения откуда корни приобретут значений Первая значение отвергаем, оно меняет суть задачи (сначала имеем снижение, а затем рост процентов, противоречит условию). Второе при пересчете составит 0,2*100%=20% процентов.

Задача 3. (558) Вкладчик положил в банк 4000 грн. За первый год ему начислена определенный процент годовых, а второго года банковский процент увеличен на 4%. На конец второго года на счете стало 4664 грн. Сколько процентов составила банковская ставка в первый год?

Решение: Обозначим через X – увеличение вклада в первый год, тогдаX+4/100%=X+0,04 начисления во второй год. По условию задачи составляем уравнение для определения неизвестной X После упрощений получим квадратное уравнение вида Вычисляем дискриминант и корни уравнения Первый корень отбрасываем, второй соответствует ставке в 6% годовых.

Задача 4. (564) В сосуде 12 кг кислоты. Часть кислоты отлили и долили до прежнего уровня водой. Затем снова отлили столько же, как и в первый раз, и долили водой до прежнего уровня. Сколько литров жидкости отливали каждый раз, если в результате получили 25-процентный раствор кислоты?

Решение: Обозначим через X – часть кислоты, которую отливали. После первого раза ее осталось 12-X, а процентное содержание кислоты После второй попытки содержание кислоты в сосуде составило. Разведя водой до 12 кг, процентное содержание составляло 25%. Составляем уравнение Упрощаем проценты и избавляемся знаменателей Решаем квадратное уравнение Условии задачи удовлетворяет второе решение, а это значит, что каждый раз отливали 6 кг жидкости. На этом знакомство со сложными процентами завершается. На практике Вам встретятся как простые так и сложные задачи. При проблемах с вычисления сложных процентов обращайтесь к нам, мы поможем Вам в решении задач.

Отзывы о Альфа банк Уфа

Для кого доступна система «Форсаж»?

Ипотечный калькулятор

Как начисляются проценты по вкладам

S=D*(P/100), где:

• S – итоговая сумма, по окончании срока действия договора;
• D – сумма инвестиций;
• P – годовой процент.

Что касается индивидуальных условий банковского обслуживания, то всё зависит от внутреннего регламента коммерческой организации. То есть, некоторые банки начисляют доход по окончании срока действия договора, другие кредитно-финансовые организации рассчитывают доход с определенной периодичностью, например, один раз в месяц, квартал или полугодие. Соответственно, клиент может получать свое вознаграждение на протяжении срока действия договора.

Кроме всего прочего, в банковской терминологии применяются такие понятия, как фиксированный и плавающий годовой процент. Фиксированное значение — это то, которое действует от начала до конца срока вложений и может измениться только при том обстоятельстве, если предусмотрена автоматическая пролонгация договора. По той причине, что в данном случае банк устанавливает тот процент, который действует на дату пролонгации.

Посчитать проценты за месяц достаточно просто, нужно применить формулу, указанную выше, но с небольшой корректировкой: S=D*(P/100/12), то есть вклад с вышеуказанными параметрами принесет своему владельцу доход в размере 67 рублей.

Формула сложного процента

Формула сложного процента позволяет быстро и просто посчитать любую задачу на вклады. Выглядит эта формула так:

$S=X*(1+m)^{n}$, где

S – итоговая сумма вклада

Х – начальная сумма вклада

m-процент в виде десятичной дроби

n-количество периодов, за которые планируется получит прибыль.

Обратите внимание, что периоды могут быть месяцами, годами, неделями, кварталами и т.д. Это нужно учитывать при решении задач на сложный процент

Теперь подсчитаем, какую прибыль получит Петя за 10 лет.

X=10000

m=0,1

n=10

Подставим все в формулу:

$S=10000*{(1+0,1)^{10}}=25937 руб$ – результат округлен до целых чисел.

В процессе вычисления без калькулятора не обойтись, зато все расчеты производятся в два-три действия. Иногда по требованию учителя или составителя учебника, округление придется производить до сотых.

Что мы узнали?

Мы поговорили о том, что такое процент. Разобрались с определением сложного процента и привели формулу сложного процента. Привели небольшой пример сложного процента, результат которого нашли с помощью формулы.

1. Вопрос 1 из 5

Начать тест(новая вкладка)

Формулы и примеры расчета процентов по договору займа

В договоре займа практически всегда указывается размер платы за использование предоставленных средств. Если об этом в документе ничего не сказано, проценты будут выплачиваться согласно текущей ставке рефинансирования.

Договор займа может быть безвозмездным только если это четко прописано в документе. Вопрос о том, как правильно рассчитать проценты по договору займа, может возникнуть, если заемщик желает убедиться в правильности всех подсчетов платежей, или же если величина переплаты вообще не была определена заранее.

Самостоятельный расчет процентов осуществляется на основе информации, содержащейся в документах, а именно:

• суммы предоставленных средств;
• процентной ставки (ежедневной, ежемесячной или годовой);
• срока предоставления средств (календарные дни, за которые начисляются проценты);
• переплата (если указывается);
• количество дней в текущем году и конкретном месяце.

Если документом предусмотрено начисление процентов за нарушение сроков, производить расчет нужно, исходя из данной ставки.

Определить проценты по договору займа можно двумя способами:

• воспользоваться сервисом расчета процентов по договору займа онлайн;
• самостоятельно произвести все вычисления.

Первый вариант выглядит несколько привлекательнее, так как ничего не нужно делать, кроме как ввести исходные данные. Найти подобный сервис не составит труда – сейчас на просторах сети имеется масса кредитных калькуляторов.

Второй способ расчета хоть и сложнее, зато надежнее

К тому же можно учесть те факторы, которые не берут во внимание онлайн сервисы. Для начала рассмотрим способ подсчета процентов по займу при условии, что в документе ставка не указана. Если процентная ставка в договоре указана, используется та же формула, что и в предыдущем примере, только вместо ставки рефинансирования указываем нужное значение

Если процентная ставка в договоре указана, используется та же формула, что и в предыдущем примере, только вместо ставки рефинансирования указываем нужное значение.

10000*2% = 200;

200*14 = 2800.

Простые

Суть простых процентов заключается в том, что ставка начисляется на одну и ту же денежную сумму. Например, если заемщик одолжил 30000 рублей, проценты будут начисляться на все эти 30000.

где:Кс – итоговая сумма, которую получает заимодавец по окончании периода начисления,С – начальная сумма долга,Т – период (в днях), в течение которого начисляются проценты,Тгод – количество дней в году,Пс – процентная ставка.

Для краткосрочных финансовых операций (например, займов на год или меньше) чаще всего используют метод исчисления простых процентов.

Это объясняется несколькими причинами:

• во-первых, расчеты по простым процентам сделать намного проще, нежели производить вычисления с применением методики сложных процентов;
• если рассматривать непродолжительные займы (до одного года), то результаты вычислений по простым и сложным процентам будут довольно близки (расхождения составляют до 1%). Данное правило справедливо при условии, что займ выдается под небольшие проценты (до 30%);
• третья и самая главная причина заключается в том, что общая задолженность по займам менее года, подсчитанная с помощью «простой» методики, выходит больше, чем, если бы долг считали по формуле сложных процентов. Именно поэтому кредиторы отдают предпочтение первому варианту.

Сложные

Некоторые финансовые организации прибегают к методике начисления сложных процентов, которая заключается в следующем: проценты прибыли по истечении каждого периода складываются с исходной суммой, и полученный результат становится основой для подсчета новых процентов.

Если документ предусматривает выплату процентов каждый месяц, но клиент по какой-либо причине допускает просрочку, к сумме заемных средств прибавляются неуплаченные проценты.

Это означает, что к следующему платежу проценты будут рассчитываться по возросшей сумме основной задолженности. Таким образом, несколько нарушений подряд приводят к стремительному расширению базы для подсчета процентов.

Кредитор также имеет право потребовать выплату неустойки или полный возврат заемных средств со всеми начисленными процентами.

s – годовая или ежемесячная ставка,n – число истекших месяцев или лет.

Таким образом, если займ составил 10000 рублей, через 12 месяцев придется отдать 13600 рублей.

Получается, что через год нужно будет вернуть уже 14258 рублей (если первоначальная сумма составила 10000 рублей). Разница между 14258 и 13600 рублями небольшая, но все же она есть.

Иногда кредиторы применят комбинированную схему начисления процентов, однако, для краткосрочных займов такой способ расчета практически не используется.

Газпромбанк Автодрайв Platinum Credit — 10 % бонусами на АЗС «Газпромнефть»

Какой метод начисления процентов более выгодный

Гражданин не может выбрать вид платежей при покупке товара в рассрочку, оформлении микрозайма. Если заемщик решил взять автокредит или получить ипотеку, то ему могут предложить на выбор дифференцированную или аннуитетную схему погашения задолженности. Плюсы и минусы обоих методов расчета процентов:

Метод расчета процентов	Преимущества	Недостатки
Аннуитетный	одинаковый размер платежей на протяжении всего срока погашения задолженности; можно оформить кредит на более крупную сумму; удобно планировать бюджет, т.к. размер выплат одинаковый.	переплата по кредиту больше; платежи со временем не уменьшаются.
Дифференцированный	меньше переплата; ежемесячные взносы постоянно уменьшаются; простой алгоритм подсчета.	большой первоначальный взнос; увеличенный размер выплат первые месяцы; максимальная сумма кредита будет меньше.

Критерии выбора процентной ставки

Прежде, чем оформить кредит в выбранном банке, стоит ознакомиться с условиями кредитования. При выборе способа начисления процентов надо учесть:

• Возможность досрочного погашения долга. Некоторые банки запрещают клиентам погашать кредит, пока не пройдет определенный период времени. Например, если ссуда взята на 2 года, то досрочно погасить ее можно будет через год. В некоторых учреждениях закрытие займа задолго до конца срока сопровождается дополнительной комиссией.
• Регулярность и величину собственного ежемесячного дохода.

Дифференцированные платежи выгодны, если заемщик собирается погашать кредит на протяжении всего срока его действия, потому что итоговый размер переплаты будет меньше.

Если же гражданин собирается быстро выплатить долг, то можно выбрать аннуитетную систему, т.к. при досрочном погашении сумма процентов будет меньше.

Формула начисления сложных процентов

Формула сложных процентов применяется при капитализации процентов (начисления процентов на проценты), т.е. начисление процентов по депозиту происходит через равные промежутки времени, а начисленные проценты прибавляются ко вкладу.

Расчет наращенной суммы вклада (сложные проценты)

Наращенная сумма при периоде начисления в годах определяется

S = P × (1 + i)n.

Пример расчета наращенной суммы при сложных процентах

Первоначальная сумма вклада P = 25000 руб., помещена в банк на n = 3 года под i = 7,5% годовых. Определим наращенную сумму

S = 25000 × (1 + 0,075)3 = 31057 руб.

Расчет периода начисления в годах при сложных процентах

Если мы знаем первоначальную сумму вклада P, наращенную сумму S и сложную годовую процентную ставку i, то определим период начисления n (в годах) по формуле

n = ln(S/P)/ln(1 + i).

Пример расчета периода начисления при сложных процентах

Первоначальная сумма вклада P = 27500 руб., наращенная сумма S = 33700 руб., i = 10% годовых. Определим за какой период была начислена сумма

S = ln(33700/27500)/ln(1 + 0,1)= 2,1 года.

Расчет годовой процентной ставки при сложных процентах

Определить годовую процентную ставку при сложных процентах можно по формуле

i = n√S/P — 1.

Пример расчета годовой процентной ставки при сложных процентах

Первоначальная сумма вклада P = 75000 руб., наращенная сумма S = 97000 руб., период начисления n = 2 года. Определим процентную ставку

i = 2√97000/75000 — 1 =0,136 = 13,6%.

Расчет наращенной суммы при плавающей процентной ставки сложных процентов

S =P × (1 + i₁)n₁ × (1 + i₂)n₂ × … × (1 + i_n)n_k

Пример расчета наращенной суммы при плавающей процентной ставки сложных процентов

Первоначальная сумма вклада P = 35000 руб., n1 = 2 года применялась сложная процентная ставка i1 = 10% годовых, затем n2 = 3 года применялась сложная процентная ставка i2 = 12% годовых. Определим наращенную сумму

S =35000 × (1 +0,1)2 × (1 +0,12)3 = 59498 руб.

 Начисление сложных процентов несколько раз в году

Если начисление сложных процентов происходит несколько раз в году, то воспользуемся формулой

S = P × (1 + j/m)n×m

где j — номинальная процентная ставка; m — интервал начисления.

Пример начисление сложных процентов несколько раз в году

Первоначальная сумма инвестирования 62000 руб., период начисления 3 года, сложная процентная ставка j = 9% годовых ежеквартально, m = 4, т.к. в году 4 квартала. Определим наращенную сумму.

S = 62000 × (1 +0,09/4)3×4 = 80975 руб.

Топ 10 вкладов на сегодня

Открыть вклад в руб.

Ставка в год7,40%Срок вклада367 дней	Льготное расторжение % в конце срока Особые условия: вклад открывается при условии заключения Договора накопительного страхования жизни
Ставка в год7,10%Срок вклада181 день	Досрочное расторжение % в конце срока Особые условия: вклад открывается не позднее трех рабочих дней с момента заключения программы инвестиционного/накопительного страхования жизни
Ставка в год7,00%Срок вклада367 дней	Досрочное расторжение % в конце срока Особые условия: вклад открывается при условии одновременного оформления договора накопительного и/или инвестиционного страхования жизни с компанией ООО СК «Росгосстрах Жизнь»
Ставка в год7,00%Срок вклада395 дней	Досрочное расторжение % в конце срока Особые условия: вклад открывается при условии заключения договора инвестиционного или накопительного страхования жизни
Ставка в год7,00%Срок вклада367 дней	Досрочное расторжение % в конце срока Особые условия: открытие вклада осуществляется по ставке, действующей в банке на момент заключения договора банковского вклада, при одновременном соблюдении следующих условий:с компанией ООО…
Ставка в год7,00%Срок вклада181 день	Досрочное расторжение % в конце срока Особые условия: в день заключения договора вклада необходимо одновременное оформление Инвестиционного продукта у одного из партнёров Банка (ООО «АльфаСтрахование-Жизнь» или ООО «Компания БКС»)…
Ставка в год7,00%Срок вклада181 день	Досрочное расторжение % в конце срока Особые условия: открывается при одновременном оформлении инвестиционного продукта у одного из партнеров банка — ООО «АльфаСтрахование-Жизнь» или ООО «Компания БКС»
Ставка в год6,75%Срок вклада181 день	Досрочное расторжение % в конце срока Особые условия: открывается при оформление полиса инвестиционного страхования жизни ООО «МАКС-Жизнь»
Ставка в год6,60%Срок вклада181 день	Досрочное расторжение % в конце срока Особые условия: открывается при предъявлении вкладчиком:договора (полиса) инвестиционного страхования жизни «Верное решение» АО «УРАЛСИБ Жизнь» сроком на 5 лет в российских рублях;договора (полиса)…
Ставка в год6,60%Срок вклада366 дней	Льготное расторжение % в конце срока Особые условия: открытие вклада возможно при одновременном оформлении полиса накопительного страхования жизни одной из страховых компаний – партнеров Банка на сумму ежегодного взноса,…

Как на практике сравнить сложные и простые проценты?

Существует два вида процентов по депозитам или вкладам — простой и сложный. О первом из них говорить долго не приходится, так как простой процент довольно-таки легко посчитать.

Сложный процент — это такой вид начисления, который увеличивает на свой размер тело депозита без разрывания договора вклада. Также его называют депозитом с капитализацией.

https://www.youtube.com/watch?v=ytpolicyandsafetyru

То есть при ставке в 20% с капитализацией условие о том, что в конце периода вы получите на такой же процент больше денег, не действует.

На практике мы встречаемся с банками, которые не желают работать себе в убыток. Согласно расчётам, которые осуществлены выше, депозиты со сложной ставкой менее выгодны для любого банка.

Практическая выгода

Идеальной формулы для начисления процентов по вкладу нет, так как все зависит от конкретных обстоятельств. Если сумма вклада будет относительно небольшой, то принципиальной разницы между стандартным депозитом и депозитом с капитализацией вклада не будет. Совсем другое дело, когда вкладчик оформляет депозит со значительной суммой. Простой подсчет только подтвердит всю выгоду капитализации. Но нельзя не отбрасывать и то, что в банке сидят далеко не глупые люди.

Тут имеется в виду то, что в независимости от депозитных предложений и от используемых при их формировании формул, банк все равно будет оставаться в плюсе для себя. Если проанализировать все предложения, которые есть на рынке, то выяснится, что практически везде процентная ставка у вкладов, имеющих капитализацию, всегда ниже, чем у классических вкладов. Тем самым соблюдается определенный баланс.

Представители банка заранее анализируют потенциальные прибыли, соответственно, заработать больше того, что было заранее просчитано, просто не получится. Но про это думать не нужно. Ломать голову приходится в том случае, когда вклад с простым и сложным начислением имеет одинаковую процентную ставку. Чаще всего делают выбор в пользу второго предложения, но везде есть свои нюансы.

Разница роста капитала при расчете в годах и при ежемесячной капитализации процентов

При желании получить ощутимую выгоду, имеет смысл ориентироваться на депозиты с капитализацией, оформляемые на год. И тогда несколько заниженный процент по ставке, по сравнению с классическими депозитами, не сыграет особой роли. Разницу в деньгах при сроке депозита в 6 месяцев также можно будет увидеть, но впечатлять она уже не будет. Чем дольше средства будут лежать на депозите, тем в итоге будет выгоднее для вкладчика.

Расчетные вклады подразумевают возможность снятия определенной суммы раньше положенного срока, при этом нельзя трогать неснижаемый остаток. Операции по депозиту никак не сказываются на размере процентной ставки. Также можно и пополнить вклад без штрафных санкций со стороны банка. Иногда банк намеренно ограничивает всевозможные действия с депозитом, например, пополнение или снятие средств доступно не более одного раза в месяц, но и этого вполне достаточно.

Валюта сети

Минусы и скрытые нюансы

Причины, влияющие на выбор клиентов в пользу других банковских продуктов:

1. Отсутствие возможности снимать и использовать начисленные проценты до окончания действия договора.
2. Невозможность или невыгодные условия расторжения соглашения, досрочного или частичного снятия средств.
3. Менее выгодные ставки, чем по обычным депозитам.
4. Отсутствие уверенности в материальной стабильности банка.
5. Наличие скрытых платежей и комиссий, таких как оплата за открытие и обслуживание счета, мобильный банкинг, комиссия за зачисление и снятие средств. Дополнительные расходы не всегда прописываются в договоре и часто относятся к категории расчетно-кассового обслуживания.
6. Право банка менять процентную ставку в процессе действия договора, о чем клиент не всегда получает своевременное уведомление.

Рыночная процентная ставка как важнейший макроэкономический показатель

Важным выступает процентная ставка. Процентная ставка — это плата за деньги, предоставляемые в . Были времена, когда законом не допускалось вознаграждение за то, что неизрасходованные, заемные деньги давали в заем. В современном мире широко пользуются кредитами, за пользование которыми устанавливается процент. Поскольку процентные ставки измеряют издержки использования денежных средств предпринимателями и вознаграждение за неиспользование денег потребительским сектором, то уровень процентных ставок играет значительную роль в экономике страны в целом.

Очень часто в экономической литературе пользуются термином «процентная ставка», хотя существует множество процентных ставок. Дифференциация процентных ставок связана с риском, на который идет заимодатель. Риск возрастает с увеличением срока кредита, так как становится выше вероятность того, что деньги могут потребоваться кредитору раньше установленной даты возврата ссуды, соответственно повышается процентная ставка. Она увеличивается, когда за кредитом обращается малоизвестный предприниматель. Мелкая фирма уплачивает более высокую процентную ставку, чем крупная. Для потребителей процентные ставки также варьируются.

Однако как бы ни отличались ставки процента, все они находятся под воздействием : если предложение денег уменьшается, то процентные ставки увеличиваются, и наоборот. Именно поэтому рассмотрение всех процентных ставок можно свести к изучению закономерностей одной процентной ставки и в дальнейшем оперировать термином «процентная ставка»

Различают номинальные и реальные процентные ставки

Реальная процентная ставка
определяется с учетом уровня . Она равна номинальной процентной ставке, которая устанавливается под воздействием спроса и предложения, за вычетом уровня инфляции:

Если, например, банк предоставляет кредит и взимает при этом 15%, а уровень инфляции составляет 10%, то реальная процентная ставка равна 5% (15% — 10%).

Капитализация процентов

На самом деле вклады под сложные проценты принято называть вклад с капитализацией процентов. Что это такое? Если говорить просто, то для вкладчика это означает начисление процентов на проценты. Например, по условиям банковского вклада прибыль от депозита начисляется ежемесячно, но, постольку, поскольку она остается не востребована вкладчиком, ее банк прибавляет к телу депозита.

Здесь размер прибыли во многом зависит от количества периодов капитализации. Многие крупные банки, в частности, Сбербанк России, ВТБ 24 и другие, предлагают своим клиентам капитализацию один раз в квартал, то есть каждые 3 месяца. А другие коммерческие банки могут вовсе рассчитывать прибыль один раз в год, соответственно, первая капитализация будет только через 12 месяцев, а именно на этот срок большинство заключает договор.

S=D×(1 N×L100×365)^x, где:

• S – общая сумма денежных средств, подлежащая возврату вкладчику по истечении срока действия депозитного договора;
• N – годовой процент без учета капитализации;
• L – число дней в том периоде, за который банк проводит капитализацию процентов;
• x – количество капитализаций за весь период действия договора;
• D – сумма инвестиций в банковский вклад.

Попробуем по данной формуле рассчитать депозит со следующими параметрами:

• сумма инвестиций — 10000 рублей;
• капитализация осуществляется один раз в месяц (всего в году 365 дней), соответственно здесь L будет равно 365/12=30,41;
• количество капитализации — 12;
• годовая ставка — 8%;

S=10000×(1 8×30,41100×365)^12= 10830 рублей – это общая прибыль по депозиту на конец срока действия договора.

Как видно, посчитать самостоятельно прибыль от депозита не так сложно. Но банки рассчитывают доход вкладчика с учетом капитализации процентов несколько по-другому. То есть, от базовой процентной ставки высчитывается эффективный процент по вкладу, то есть тот который будет действовать с учетом причисления процентов к телу депозита на протяжении срока действия депозитного договора.

((1 P/12)^x-1)×12/x, где:

• P – это годовой процент без учета капитализации;
• x – количество периодов капитализации (при том условии, если она осуществляется ежемесячно).

((1 8/100/12)^ 12-1)×12/12=0,083.

((1 P/100/4)^4-1)×100%.

Считаем вклад с теми же параметрами ((1 8/100/4)^4-1)×100%=0,2682417945625, или приблизительно 0,268.

Послесловие

В рамках данного обзора, вы узнали что такое капитализация процента, какова формула сложных процентов, а так же увидели пример с расчетом, демонстрирующим разницу в доходе.

Хоть, сложные проценты и могут представлять интерес, всегда важно помнить про здравую логику и то, что у вас своя голова. Во-первых, могут присутствовать различные тонкости (что и когда можно снимать, что происходит если снять деньги раньше, некратные периоды и так далее)

Во-вторых, чрезмерные сложности при расчетах и сравнении, особенно если используются дробные цифры (например, 6,03% в год с ежегодной капитализацией за 10 лет составит примерно 79,6% дохода, а вот 5,96% при ежемесячной капитализации составит 81,2%). Подобные вещи непросто заметить обычному человеку.

В-третьих, капитализация предусматривает автоматическое повторное вложение денег, в то время как простые проценты могут подразумевать возможность использовать доход для иных целей. И так далее.

Что из себя представляют сложные проценты?

Сложный процент — это особый вид накопления при оформлении банковского вклада. Проценты при таком депозите начисляются регулярно по истечении определённого периода (раз в месяц или один раз в 3 месяца). При этом следующее начисление будет производиться на сумму, полученную в результате предыдущих начислений. За счёт капитализации вкладчики получают большую выгоду, так как в этом случае сумма вклада растёт значительно быстрее. Процесс начисления в этом случае называется реинвестированием или капитализацией.

Такие проценты имеют множество различных названий. В зависимости от сферы деятельности можно встретить следующие названия представленного термина:

• эффективный;
• композиционный;
• норма доходности реинвестирования;
• норма доходности капитализации.

Чтобы лучше понять, в чём заключается схема сложных процентов, необходимы определённые знания из области банковской математики. При вычислении депозита берутся следующие параметры: капитал, частота выплат, размер ставки по вкладу, период ставки и срок, на который открывается вклад. Сравнив депозиты с различными начислениями по этим параметрам, можно прийти к следующим выводам:

1. Если оформить вклад с простым начислением, то деньги будут начисляться на основной капитал. При этом период вложения не играет никакой роли. В этом случае сумма депозита будет увеличиваться по модели арифметической прогрессии.
2. Если же оформить вклад со сложным начислением, то деньги будут начисляться по окончании установленного периода и прибавляться к вложенному капиталу. За счёт этого в последующих периодах проценты станут высчитываться из новой суммы депозита. Благодаря этому рост суммы депозита будет с каждым разом увеличиваться со скоростью экспоненты.

Сводка по кредиту

Расчет банковских процентов по вкладам — формула

Исходя из положений п. 1 ст. 838 Гражданского кодекса Российской Федерации (ГК РФ), формула расчета банковских процентов по вкладам зависит от того, как процент по вкладу определен в соглашении сторон.

Так, если процент прямо в договоре не установлен, то с учетом п. 1 ст. 809 ГК РФ он определяется на основании ставки банковского процента по месту нахождения вкладчика на дату выплаты денег. При этом особенности расчета процента могут иметь место в зависимости от того, открыт классический вклад или заведена сберегательная книжка, приобретен ли сберегательный сертификат.

Помимо собственно размера процента, для произведения расчета необходимо определить период, за который начисляются проценты, а также сумму, на которую они начисляются (включает она начисленные ранее проценты или ограничивается изначально внесенной суммой).

ВАЖНО! Согласно п. 1 ст. 839 ГК РФ день внесения банковского вклада для расчета процентов не учитывается, в то время как день выдачи денег включается в расчет.

В соответствии с п. 2 указанной статьи проценты выплачиваются ежеквартально или входят в общую сумму для расчета последующих процентов, если не были востребованы вкладчиком. Иной порядок может быть определен соглашением сторон.

Что такое прогрессивное начисление по банковскому вкладу

Прогрессивное начисление как таковое используется в праве не только применительно к банковским вкладам.

Так, при взыскании денежных средств, присуждаемых за неисполнение судебного акта, в судебной практике, в частности, встречается такой подход, как установление прогрессивного начисления. Например, если за каждый последующий период неисполнения взыскивается сумма больше, чем предполагалась за неисполнение в менее продолжительные периоды просрочки (постановление 18-го арбитражного апелляционного суда от 26.06.2015 № 18АП-6587/2015 по делу № А07-4912/2014).

Применительно к банковским вкладам прогрессивное начисление может означать, например, отличие размера процентов в зависимости от суммы остатка на депозите (письмо Минфина РФ от 05.12.2011 № 03-04-06/6-332). Помимо роста ставки с ростом суммы на депозите, прогрессивное начисление процентов по вкладу может применяться в зависимости от срока вклада, например увеличение процентной ставки при превышении годичного срока вклада.

Прогрессивное начисление по банковскому вкладу как нарастание ставки в зависимости от времени, когда вклад востребуется вкладчиком, признается экспертами в качестве одного из механизмов, используемых банками для снижения рисков в своей профессиональной деятельности (п. 5 экспертного заключения по проекту Федерального закона «О внесении изменений в ст. 837 ГК РФ», принятого на заседании Совета при Президенте РФ по кодификации и совершенствованию гражданского законодательства 17.11.2003).