Java math.round function

Округление при работе с числами ограниченной точности

Реальные физические величины всегда измеряются с некоторой конечной точностью, которая зависит от приборов и методов измерения и оценивается максимальным относительным или абсолютным отклонением неизвестного истинного значения от измеренного, что в десятичном представлении значения соответствует либо определённому числу значащих цифр, либо определённой позиции в записи числа, все цифры после (правее) которой являются незначащими (лежат в пределах погрешности измерения). Сами измеренные параметры записываются с таким числом знаков, чтобы все цифры были надёжными, возможно, последняя — сомнительной. Погрешность при математических операциях с числами ограниченной точности сохраняется и изменяется по известным математическим законам, поэтому когда в дальнейших вычислениях возникают промежуточные значения и результаты с больши́м числом цифр, из этих цифр только часть являются значимыми. Остальные цифры, присутствуя в значениях, фактически не отражают никакой физической реальности и лишь отнимают время на вычисления. Вследствие этого промежуточные значения и результаты при вычислениях с ограниченной точностью округляют до того количества знаков, которое отражает реальную точность полученных значений. На практике обычно рекомендуется при длинных «цепочных» ручных вычислениях сохранять в промежуточных значениях на одну цифру больше. При использовании компьютера промежуточные округления в научно-технических приложениях чаще всего теряют смысл, и округляется только результат.

Так, например, если задана сила 5815 гс с точностью до грамма силы и длина плеча 1,40 м с точностью до сантиметра, то момент силы в кгс по формуле M=(mg)⋅h{\displaystyle M=(mg)\cdot h}, в случае формального расчёта со всеми знаками, окажется равным: 5,815 кгс • 1,4 м = 8,141 кгс•м. Однако если учесть погрешность измерения, то мы получим, что предельная относительная погрешность первого значения составляет 1/5815 ≈ 1,7•10−4, второго — 1/140 ≈ 7,1•10−3, относительная погрешность результата по правилу погрешности операции умножения (при умножении приближённых величин относительные погрешности складываются) составит 7,3•10−3, что соответствует максимальной абсолютной погрешности результата ±0,059 кгс•м! То есть в реальности, с учётом погрешности, результат может составлять от 8,082 до 8,200 кгс•м, таким образом, в рассчитанном значении 8,141 кгс•м полностью надёжной является только первая цифра, даже вторая — уже сомнительна! Корректным будет округление результата вычислений до первой сомнительной цифры, то есть до десятых: 8,1 кгс•м, или, при необходимости более точного указания рамок погрешности, представить его в виде, округлённом до одного-двух знаков после запятой с указанием погрешности: 8,14 ± 0,06 кгс•м.

Округление рассчитанного значения погрешности

Обычно в окончательном значении рассчитанной погрешности оставляют только первые одну-две значащие цифры. По одному из применяемых правил, если значение погрешности начинается с цифр 1 или 2(по другому правилу — 1, 2 или 3), то в нём сохраняют две значащих цифры, в остальных случаях — одну, например: 0,13; 0,26; 0,3; 0,8. То есть каждая декада возможных значений округляемой погрешности разделена на две части. Недостаток этого правила состоит в том, что относительная погрешность округления изменяется значительным скачком при переходе от числа 0,29 к числу 0,3. Для устранения этого предлагается каждую декаду возможных значений погрешности делить на три части с менее резким изменением шага округления. Тогда ряд разрешённых к употреблению округлённых значений погрешности получает вид:

• 0,10; 0,12; 0,14; 0,16; 0,18;
• 0,20; 0,25; 0,30; 0,35; 0,40; 0,45;
• 0,5; 0,6; 0,7; 0,8; 0,9; 1,0.

Однако при использовании такого правила последние цифры самого результата, оставляемые после округления, также должны соответствовать приведённому ряду.

Пересчёт значений физических величин

Пересчёт значения физической величины из одной системы единиц в другую должен производиться с сохранением точности исходного значения. Для этого исходное значение в одних единицах следует умножить (разделить) на переводной коэффициент, часто содержащий большое количество значащих цифр, и округлить полученный результат до количества значащих цифр, обеспечивающего точность исходного значения. Например, при пересчёте значения силы 96,3 тс в значение, выраженное в килоньютонах (кН), следует умножить исходное значение на переводной коэффициент 9,80665 (1 тс = 9,80665 кН). В результате получается значение 944,380395 кН, которое необходимо округлить до трёх значащих цифр. Вместо 96,3 тс получаем 944 кН.

Различие округления в Python 2 и Python 3

В Python 2 и Python 3 реализованы разные принципы округления.

В Python 2 используется арифметическое округление. В нем наблюдается большое количество погрешностей, что приводит к неточностям в процессе вычислений.

Во втором Python есть только 4 цифры, которые ведут к преобразованию к меньшему значению – 1, 2, 3 и 4. Также 5 цифр, которые приводят к большему значению – 5, 6, 7, 8, 9. Такое неравное распределение ведет к тому, что погрешность постоянно нарастает.

Python 2 по правилам арифметического округления преобразует число 5,685 в 5,68 до второго знака. Такая погрешность связана с тем, что десятичные цифры float в двоичном коде невозможно корректно представить.

В Python 3 используются принципы банковского округления. Это означает, что преобразование производится к ближайшему четному. В таком случае также не удается полностью избежать возникающих ошибок, но программисты добиваются точности в подсчетах.

2,5 по правилам банковского преобразования будет равно 2, а 3,5 = 4 (значения возводятся к близкому четному). Минимизировать погрешности можно благодаря практически равной вероятности, что перед пятеркой будет четное или нечетное число.

Java Math.round on Array example

In this Java program, we find the rounded values of bulk data. Here, we are going to declare an array of double type and find the closest (rounded) values of array elements using java math.round.

OUTPUT

ANALYSIS

Within this Java round example, we declared an Array of double type and assigned some random values.

Next, We used the Java For Loop to iterate the Array. Within the For Loop, we initialized the i value as 0.

Next, compiler will check for the condition (i < myArray.length). As along the condition is True statement inside the for loop executed.

TIP: myArray.length finds the length of the Java array.

The following statements will print the output. If you observe the code snippet, we used the round Function directly inside System.out.format statement.

Here, the compiler will call the Java Math.round method ( static long round(double number) ) to find the corresponding closet (rounded) values.

NOTE: To find the closet (rounded) value of a single item, then use: Math.round(myArray)

Округление десятичных дробей

Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление. Цифра, записанная в данном разряде:

• не меняется, если следующая за ней справа цифра — 0, 1, 2, 3 или 4;
• увеличивается на единицу, если следующая за ней справа цифра — 5,6,7,8 или 9.

Все цифры, стоящие справа от данного разряда, заменяются нулями. Если эти нули находятся в дробной части числа, то их не пишут.

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра в предыдущем разряде (слева) увеличивается на 1.

Округление чисел особенно часто требуется при денежных расчетах. Например, цену товара в рублях, как правило, нельзя устанавливать с точностью более двух знаков после запятой. Если же в результате вычислений получается большее число десятичных разрядов, требуется округление. В противном случае накапливание тысячных и десятитысячных долей рубля приведет в итоге к ошибкам в вычислениях.

Для округления чисел можно использовать целую группу функций.

Наиболее часто используют функции ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ.

Синтаксис функции ОКРУГЛ

ОКРУГЛ(А;В),

где A – округляемое число;

Синтаксис функций ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ точно такой же, что и у функции ОКРУГЛ.

Функция ОКРУГЛ при округлении отбрасывает цифры меньшие 5, а цифры большие 5 округляет до следующего разряда. Функция ОКРУГЛВВЕРХ при округлении любые цифры округляет до следующего разряда. Функция ОКРУГЛВНИЗ при округлении отбрасывает любые цифры. Пример округления до двух знаков после запятой с использованием функций ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ приведен на рис. 7.4.

Рис. 7.4.
Округление до заданного количества десятичных разрядов

Функции ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ можно использовать и для округления целых разрядов чисел. Для этого необходимо использовать отрицательные значения аргумента В.

Для округления чисел в меньшую сторону можно использовать также функцию ОТБР.

Синтаксис функции

ОТБР(А;В),

где A – округляемое число;

В – число знаков после запятой (десятичных разрядов), до которого округляется число.

Фактически функция ОТБР отбрасывает лишние знаки, оставляя только количество знаков, указанное в аргументе В.

Так же как и функции ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, функцию ОТБР можно использовать для округления целых разрядов чисел. Для этого необходимо использовать отрицательные значения аргумента В.

Для округления числа до меньшего целого можно использовать функцию ЦЕЛОЕ.

Синтаксис функции

где A – округляемое число.

Пример использования функции приведен на рис. 7.5.

Рис. 7.5.
Округление до целого числа

Для округления числа с заданной точностью можно использовать функцию ОКРУГЛТ.

Синтаксис функции

ОКРУГЛТ(А;В),

где A – округляемое число;

В – точность, с которой требуется округлить число.

Функция ОКРУГЛТ производит округление с избытком. Округление производится в том случае, если остаток от деления числа на точность больше или равен половине точности. Пример использования функции приведен на рис. 7.6.

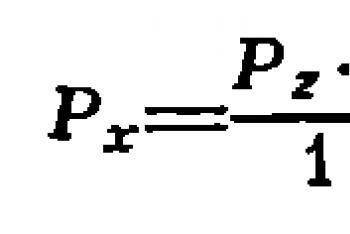
Рис. 7.6.
Округления с заданной точностью

Наконец, для округления до ближайшего четного или нечетного числа можно использовать функции ЧЕТН и НЕЧЕТН, а для ближайшего кратного большего или меньшего числа – функции ОКРВЕРХ и ОКРВНИЗ.

Синтаксис функции ЧЕТН

где A – округляемое число.

Функция НЕЧЕТН имеет такой же синтаксис.

Обе функции округляют положительные числа до ближайшего большего четного или нечетного числа, а отрицательные – до ближайшего меньшего четного или нечетного числа.

Синтаксис функции ОКРВВЕРХ

ОКРВВЕРХ(А;В),

где A – округляемое число;

В – кратное, до которого требуется округлить.

Функция ОКРВНИЗ имеет такой же синтаксис.

Следует обратить внимание на различие в округлении и установке отображаемого числа знаков после запятой с использованием средств форматирования. При использовании числовых форматов изменяется только отображаемое число, а в вычислениях используется хранимое значение

Чтобы быстро сделать так, чтобы число казалось округленным, измените количество десятичных разрядов. Просто выделите число, которое вы хотите округлить, и щелкните Главная
> Уменьшить разрядность

.

Число в ячейке будет казаться округленным, но фактическое значение не изменится — при ссылке на ячейку будет использоваться полное значение.

Rounding Doubles With BigDecimal

To round doubles to n decimal places, we can write a helper method:

There is one important thing to notice in this solution – when constructing BigDecimal; we must always use BigDecimal(String) constructor. This prevents issues with representing inexact values.

We can achieve the same by using the Apache Commons Math library:

The latest version can be found .

Once the library is added to the project, we can use the Precision.round() method, which takes two arguments – value and scale:

By default, it is using the same HALF_UP rounding method as our helper method. Therefore, the results should be the same.

Note that we can change rounding behavior by passing the desired rounding method as a third parameter.

Causes of Error Code 0xc0000001

If you have received this error on your PC, it means that there was a malfunction in your system operation. Common reasons include incorrect or failed installation or uninstallation of software that may have left invalid entries in your Windows registry, consequences of a virus or malware attack, improper system shutdown due to a power failure or another factor, someone with little technical knowledge accidentally deleting a necessary system file or registry entry, as well as a number of other causes. The immediate cause of the “Error Code: 0xc0000001” error is a failure to correctly run one of its normal operations by a system or application component.

Класс Java Math

Класс Java Math предоставляет более сложные математические вычисления, чем те, которые предоставляют базовые математические операторы Java. Класс Math содержит методы для:

• нахождения максимального или минимального значений;
• значений округления;
• логарифмических функций;
• квадратного корня;
• тригонометрических функций (sin, cos, tan и т. д.).

Math находится в пакете java.lang, а не в пакете java.math. Таким образом, полное имя класса Math — это java.lang.Math.

Поскольку многие его функции независимы друг от друга, каждый метод будет объяснен в своем собственном разделе ниже.

Overview

In this short article, we’re going to look at how to round a number to n decimal places in Java.

2. Decimal Numbers in Java

Java provides two primitive types that can be used for storing decimal numbers: float and double. Double is the type used by default:

However, both types should never be used for precise values, such as currencies. For that, and also for rounding, we can use the BigDecimal class.

3. Formatting a Decimal Number

If we just want to print a decimal number with n digits after decimal point, we can simply format the output String:

Alternatively, we can format the value with the DecimalFormat class:

DecimalFormat allows us to explicitly set rounding behavior, giving more control of the output than String.format() used above.

4. Rounding Doubles With BigDecimal

To round doubles to n decimal places, we can write a helper method:

There is one important thing to notice in this solution – when constructing BigDecimal; we must always use BigDecimal(String) constructor. This prevents issues with representing inexact values.

We can achieve the same by using the Apache Commons Math library:

The latest version can be found .

Once the library is added to the project, we can use the Precision.round() method, which takes two arguments – value and scale:

By default, it is using the same HALF_UP rounding method as our helper method. Therefore, the results should be the same.

Note that we can change rounding behavior by passing the desired rounding method as a third parameter.

5. Rounding Doubles With DoubleRounder

DoubleRounder is a utility in the decimal4j library. It provides a fast and garbage-free method for rounding doubles from 0 to 18 decimal points.

We can get the library (the latest version can be found ) by adding the dependency to the pom.xml:

Now, we can simply use:

However, DoubleRounder fails in a few scenarios, for example:

6. Math.round() Method

Another way of rounding numbers is to use Math.Round() Method.

In this case, we can control n number of decimal places by multiplying and dividing by 10^n:

This method is not recommended as it’s truncating the value. In many cases values are rounded incorrectly:

And so, this method is listed here for learning purposes only.

7. Conclusion

In this quick tutorial, we covered different techniques for rounding numbers to n decimal places.

We can simply format the output without changing the value, or we can round the variable by using a helper method. We’ve also covered a few libraries that deal with this problem.

The code used during the discussion can be found over on GitHub.

Округление

Одна из часто используемых операций при работе с числами – это округление.

В JavaScript есть несколько встроенных функций для работы с округлением:

Округление в меньшую сторону: становится , а — .

Округление в большую сторону: становится , а — .

Округление до ближайшего целого: становится , — , а — .

(не поддерживается в Internet Explorer)

Производит удаление дробной части без округления: становится , а — .

Ниже представлена таблица с различиями между функциями округления:

Эти функции охватывают все возможные способы обработки десятичной части. Что если нам надо округлить число до количества цифр в дробной части?

Например, у нас есть и мы хотим округлить число до 2-х знаков после запятой, оставить только .

Есть два пути решения:

Умножить и разделить.
Например, чтобы округлить число до второго знака после запятой, мы можем умножить число на , вызвать функцию округления и разделить обратно.

Метод toFixed(n) округляет число до знаков после запятой и возвращает строковое представление результата.

Округляет значение до ближайшего числа, как в большую, так и в меньшую сторону, аналогично методу :

Обратите внимание, что результатом является строка. Если десятичная часть короче, чем необходима, будут добавлены нули в конец строки:

Мы можем преобразовать полученное значение в число, используя унарный оператор или , пример с унарным оператором: .

1 Тригонометрические функции в Java

Ранее, когда мы изучали округление чисел, мы познакомились с классом и некоторыми его методами. Сейчас мы рассмотрим этот класс более подробно.

В классе , на что как бы намекает это название, собраны самые часто употребляемые программистами математические функции. Вот самые интересные из них:

Метод	Описание
	Возвращает синус угла , заданного в радианах
	Возвращает косинус угла , заданного в радианах
	Возвращает тангенс угла , заданного в радианах
	Возвращает арксинус
	Возвращает арккосинус
	Возвращает арктангенс
	Возвращает гиперболический синус
	Возвращает гиперболический косинус
	Возвращает гиперболический тангенс

Функции , и принимают угол заданный в радианах. Чтобы преобразовать углы из градусов в радианы и обратно, в классе есть две специальные функции:

Метод	Описание
	Преобразует угол из градусов в радианы
	Преобразует угол из радиан в градусы

В классе , кстати, есть не только функции, но еще и две переменные-константы (статические поля класса):

Константа	Описание
	Число «Пи» равное
	Число «Е» равное

Все эти функции могут быть вам очень полезны, если вы решите писать свои игры, работать с графикой, ну или просто посчитать длину пути по карте.

Например, если вы хотите вычислить , вот как можно это сделать:

Пример использования:

Как подключить джойстик к компьютеру Windows 10? Рекомендации по настройке

Суть проблемы

Когда мы начали создавать сервисы General Ledger для бухгалтерского учета, то обнаружили, что во многих местах были ошибки в 0.01 или более процентов. Это делает учёт денег практически невозможным. Кто хотел бы выставить счёт клиенту на $4.01, когда в его заказе $4.00?

Причины этих ошибок стали понятны достаточно быстро: расчёты, которые содержат суммы, количества, коррективы, и многие другие вещи обычно выполняются с малым или вообще без внимания к особенностям проблем точности и округления, которые возникают при работе с финансами.

Все эти вычисления использовали тип Java double, который не предлагает способа управления округлением числа или ограничения точности в расчётах. Мы пришли к решению, включающему использование java.math.BigDecimal, что дает нам управлять всем этим.

Эта статья — пример проблем математики финансов и учебник по использованию BigDecimal в целом.

parseInt и parseFloat

Для явного преобразования к числу можно использовать или . Если строка не является в точности числом, то результат будет :

Единственное исключение — это пробелы в начале строки и в конце, они игнорируются.

В реальной жизни мы часто сталкиваемся со значениями у которых есть единица измерения, например или в CSS. Также во множестве стран символ валюты записывается после номинала . Так как нам получить числовое значение из таких строк?

Для этого есть и .

Они «читают» число из строки. Если в процессе чтения возникает ошибка, они возвращают полученное до ошибки число. Функция возвращает целое число, а возвращает число с плавающей точкой:

Функции вернут , если не смогли прочитать ни одну цифру:

Второй аргумент

Функция имеет необязательный второй параметр. Он определяет систему счисления, таким образом может также читать строки с шестнадцатеричными числами, двоичными числами и т.д.:

Выбор способа округления

Существует несколько способов округления в зависимости от способа применения результата: округление к меньшему/ большему, округление к меньшему/ большему по модулю, округление к ближайшему целому, округление к ближайшему чётному и т. д… Округление к ближайшему целому, в свою очередь, можно делать по-разному в зависимости от того, какой результат должен получиться, если дробная часть равна 0,5. Я буду рассматривать округление к ближайшему целому, причём 0,5 будет округляться в большую (по модулю) сторону.

Требования к корректной реализации Round() заключаются в следующем:

• правильно округляет до ближайшего целого все конечные числа;
• поддерживает специальные значения (NaN, Inf, -0), возвращая их без изменений.

Я буду использовать следующие тестовые примеры для проверки корректности, в каждой паре содержатся исходное значение и предполагаемый результат выполнения функции Round():

В этом списке есть обычные числа, специальные значения и некоторые граничные случаи, с которыми простым алгоритмам сложно справиться

Обратите внимание, что, поскольку мы используем float, мы не можем использовать число 0,49999999999999999 в качестве ближайшего к 0,5, так как из-за ограниченной точности float это число в точности равно 0,5. Вместо этого я использую 0,49999999999999994

Реализации, предложенные в закрытом тикете, явно не были проверены на подобных данных, часто не работали даже те из них, которые были предложены известными людьми. Это лишний раз доказывает, насколько сложно написать Round().

int(f + 0.5)

Первая реализация, предложенная rsc, выглядела следующим образом:

Она некорректно работает с особыми значениями, отрицательными числами, числами больше math.MaxInt64 и числами, близкими к 0,5:

Floor() or Ceil()

Второй предложенный вариант учитывал отрицательные числа:

однако продолжал некорректно работать в некоторых случаях:

Первые два теста не проходят, потому что результат разности n — 0,5 равен в точности -1,0, тогда как мы ожидаем получить что-то точно большее, чем -1,0. Если посмотреть на , можно понять, как решить эту проблему.

Самое интересное, что эта ошибка не является такой уж редкой. До версии 6 точно такая же присутствовала в Java. Хорошо, что с тех пор реализация улучшилась.

int и Copysign

В третьем предложении от minux была предпринята другая попытка решить проблему отрицательных чисел:

И этот вариант всё равно ломает тесты:

Как видно, часть тестов стала проходить, однако другие начали падать. Была предпринята попытка улучшить этот алгоритм:

Однако и она провалилась:

Этот вариант выглядит лучше остальных, но и он некорректно обрабатывает особые значения и большие числа. Первую проблему можно решить с помощью дополнительных условий, но со второй справиться не так просто.

Мы рассмотрели уже четыре варианта, и в каждом из них нашлись изъяны. Настало время посмотреть, как Round() реализуют авторы различных пакетов.

Kubernetes

Kubernetes 1.7 содержит реализацию:

Она ломает следующие тесты:

Судя по тому, что функция возвращает int32, она не предназначена для работы с большими числами. Однако она некорректно работает и с числами, которые близки к 0,5.

Где делать округление: размышления о точности

Теперь, когда есть возможность управлять округлением расчёта, до какого знака следует округлять? Ответ зависит от того, как планируется использовать полученное число.

Вам известна требуемая точность конечного результата из потребностей пользователей. Для чисел, которые будут складываться и вычитаться для получения конечного результата, необходимо добавить ещё один десятичный разряд, так что сумма 0.0144 + 0.0143 будет округлена до 0.03, в то время как если округление выполняется до 0.01, результатом будет 0.02.

Если необходимы числа, которые будут умножаться для получения конечного результата, необходимо сохранять столько знаков после запятой, сколько возможно. Например, коэффициенты и удельные затраты не должны округляться. После умножения необходимо округлять конечный результат.

Математические вычисления и класс Math

Последнее обновление: 28.10.2018

Для выполнения различных математических операций в Java в пакете java.lang определен класс
Math. Рассмотрим его основные методы:

• : возвращает абсолютное значение для аргумента value

  double result = Math.abs(-13.5); // 13.5
  

• : возвращает арккосинус value. Параметр value должен иметь значение от -1 до 1

  double result = Math.acos(1); // 0.0
  

• : возвращает арксинус value. Параметр value должен иметь значение от -1 до 1

• : возвращает арктангенс value

• : возвращает кубический корень числа value

  double result = Math.cbrt(27); // 3
  

• : возвращает наименьшее целое число с плавающей точкой, которое не меньше value

  double result = Math.ceil(2.34); // 3
  

• : возвращает косинус угла d

• : возвращает гиперболический косинус угла d

• : возвращает основание натурального логарифма, возведенное в степень d

• : возвращает наибольшее целое число, которое не больше d

  double result = Math.floor(2.56); // 2
  

• : возвращает целочисленный результат деления a на b

  System.out.println(Math.floorDiv(1, 2)); // 0
  System.out.println(Math.floorDiv(7, 2)); // 3
  System.out.println(Math.floorDiv(9, 2)); // 4
  

• : возвращает натуральный логарифм числа a

• : возвращает натуральный логарифм числа (d + 1)

• : возвращает десятичный логарифм числа d

• : возвращает максимальное число из a и b

• : возвращает минимальное число из a и b

• : возвращает число a, возведенное в степень b

• : возвращает случайное число от 0.0 до 1.0

• : возвращает число double, которое представляет ближайшее к числу value целое число

  System.out.println(Math.rint(2)); // 2.0
  System.out.println(Math.rint(2.3)); // 2.0
  System.out.println(Math.rint(2.5)); // 2.0
  System.out.println(Math.rint(2.5001)); // 3.0
  System.out.println(Math.rint(2.8)); // 3.0
  

• : возвращает число d, округленное до ближайшего целого числа

  System.out.println(Math.round(2.3)); // 2
  System.out.println(Math.round(2.5)); // 3
  System.out.println(Math.round(2.5001)); // 3
  System.out.println(Math.round(2.8)); // 3
  

• : возвращает произведение числа value на 2 в степени factor

  System.out.println(Math.scalb(5, 3)); // 5*2*2*2 = 40
  System.out.println(Math.scalb(3, 4)); // 3*2*2*2*2 = 48
  

• : возвращает число 1, если число value положительное, и -1, если значение value отрицательное. Если value равно 0, то возвращает 0

  System.out.println(Math.signum(2.3)); // 1
  System.out.println(Math.signum(-2.3)); // -1
  

• : возвращает синус угла value

• : возвращает гиперболический синус угла value

• : возвращает квадратный корень числа value

  double result1 = Math.sqrt(16); // 4
  

• : возвращает тангенс угла value

• : возвращает гиперболический тангенс угла value

• переводит радианы в градусы и — градусы в радианы

  System.out.println(Math.toDegrees(3.14159)); // 180
  System.out.println(Math.toRadians(90)); // 1,57079....
  

Также класс Math определяет две константы: и . Например, вычислим площадь круга:

import java.util.Scanner;

public class Program {
  
    public static void main(String[] args) {
          
        Scanner in = new Scanner(System.in);
        
        System.out.print("Введите радиус круга: ");
        int radius = in.nextInt();
        long area = Math.round(Math.PI * Math.pow(radius, 2));
        System.out.printf("Площадь круга с радиусом %d равна %d \n", radius, area);
    }
}

Консольный вывод:

Введите радиус круга: 10
Площадь круга с радиусом 10 равна 314

НазадВперед

Способы записи числа

Представьте, что нам надо записать число 1 миллиард. Самый очевидный путь:

Но в реальной жизни мы обычно опускаем запись множества нулей, так как можно легко ошибиться. Укороченная запись может выглядеть как или для 7 миллиардов 300 миллионов. Такой принцип работает для всех больших чисел.

В JavaScript можно использовать букву , чтобы укоротить запись числа. Она добавляется к числу и заменяет указанное количество нулей:

Другими словами, производит операцию умножения числа на 1 с указанным количеством нулей.

Сейчас давайте запишем что-нибудь очень маленькое. К примеру, 1 микросекунду (одна миллионная секунды):

Записать микросекунду в укороченном виде нам поможет .

Если мы подсчитаем количество нулей , их будет 6. Естественно, верная запись .

Другими словами, отрицательное число после подразумевает деление на 1 с указанным количеством нулей:

Шестнадцатеричные числа широко используются в JavaScript для представления цветов, кодировки символов и многого другого. Естественно, есть короткий стиль записи: , после которого указывается число.

Например:

Не так часто используются двоичные и восьмеричные числа, но они также поддерживаются для двоичных и для восьмеричных:

Есть только 3 системы счисления с такой поддержкой. Для других систем счисления мы рекомендуем использовать функцию (рассмотрим позже в этой главе).

Тригонометрические функции

Класс Java Math содержит набор тригонометрических функций. Эти функции могут вычислять значения, используемые в тригонометрии, такие как синус, косинус, тангенс и т. д.

Mathkpi

Константа Math.PI представляет собой двойное значение, значение которого очень близко к значению PI — математическому определению PI.

Math.sin()

Метод Math.sin() вычисляет значение синуса некоторого значения угла в радианах:

double sin = Math.sin(Math.PI);
System.out.println("sin = " + sin);

Math.cos()

Метод Math.cos() вычисляет значение косинуса некоторого значения угла в радианах:

double cos = Math.cos(Math.PI);
System.out.println("cos = " + cos);

Math.tan()

Метод Math.tan() вычисляет значение тангенса некоторого значения угла в радианах:

double tan = Math.tan(Math.PI);
System.out.println("tan = " + tan);

Math.asin()

Метод Math.asin() вычисляет значение синусоиды значения от 1 до -1:

double asin = Math.asin(1.0);
System.out.println("asin = " + asin);

Math.acos()

Метод Math.acos() вычисляет значение арккосинуса от 1 до -1:

double acos = Math.acos(1.0);
System.out.println("acos = " + acos);

Math.atan()

Метод Math.atan() вычисляет значение арктангенса для значения от 1 до -1:

double atan = Math.atan(1.0);
System.out.println("atan = " + atan);

Вот что говорит JavaDoc:

Если вам нужен этот метод, пожалуйста, прочитайте JavaDoc.

Math.sinh()

Метод Math.sinh() вычисляет значение гиперболического синуса значения между 1 и -1:

double sinh = Math.sinh(1.0);
System.out.println("sinh = " + sinh);

Math.cosh()

Метод Math.cosh() вычисляет значение гиперболического косинуса от 1 до -1:

double cosh = Math.cosh(1.0);
System.out.println("cosh = " + cosh);

Math.tanh()

Метод Math.tanh() вычисляет значение гиперболического тангенса значения от 1 до -1:

double tanh = Math.tanh(1.0);
System.out.println("tanh = " + tanh);

Math.toDegrees()

Метод Math.toDegrees() преобразует угол в радианах в градусы:

double degrees = Math.toDegrees(Math.PI);
System.out.println("degrees = " + degrees);

Math.toRadians()

Метод Math.toRadians() преобразует угол в градусах в радианы:

double radians = Math.toRadians(180);
System.out.println("radians = " + radians);

Заключение

В этой статье я рассказывал в основном об округлении к меньшему по модулю, но есть . В некоторых случаях подходят именно они, и я оставлю читателю возможность изучить их и попробовать реализовать на Go. Но я надеюсь, что теперь вам стало понятно, как устроено округление в Go и как нужно тестировать реализации округления.

Думаю, команда Go приняла правильное решение, добавив функцию Round() в стандартную библиотеку. Без этого мы бы продолжали пользоваться различными некорректными реализациями.

Надеюсь, теперь вам стало ясно, что при работе с float есть много подводных камней, про которые порой забывают даже эксперты. Легко придумать или скопировать откуда-то однострочную реализацию, но сложно написать действительно корректную. Неудивительно, что корректно работающее округление появилось лишь в шестой мажорной версии Java (через 15 лет, прошедших с релиза Java 1.0 до выхода Java 7), и я рад, что Go прошёл этот путь быстрее.