Корреляционный анализ спирмена

11.4. Коэффициенты прямолинейной парной корреляции

Если взаимосвязь
между изучаемой парой признаков
выражается в форме, близкой к прямолинейной,
то степень тесноты связи между этими
признаками можно рассчитать при помощи
коэффициента
прямолинейной парной корреляции.
В настоящее время имеется много различных
способов расчета коэффициента парной
корреляции. Каждый способ учитывает
характер и особенности взаимосвязей
между изучаемыми признаками в
статистической совокупности. Доказано,
что наиболее точный результат
корреляционной тесноты связи между
факторным и результативным признаками
может быть получен по формуле

,
(11.2)

где r
_ху
– коэффициент парной корреляции между
признаком-фактором (х) и признаком-результатом
(у); t_x
– нормированное отклонение по
признаку-фактору; t
_y
– нормированное отклонение по
признаку-результату.

Коэффициенты
корреляции, также как и корреляционные
отношения, обладают стабильным свойством,
заключающимся в том, что пределы колебаний
этих показателей могут быть выражены
следующим образом: -1< r
_ху
< 1. Это означает, что коэффициенты
корреляции и корреляционные отношения
могут колебаться в пределах, не превышающих
единицу.

Сокращенный
вариант расчета коэффициента парной
корреляции между урожайностью сена
многолетних трав и годовым удоем коров
в 100 сельскохозяйственных организациях
по формуле 11.3 приведен в табл. 11.1.

Т
а б л и ц а 11.
1. Расчет
вспомогательных показателей для
определения коэффициента парной
корреляции

№ п.п.	х, ц/га	, ц/га		, ц/га	у, ц	, ц		, ц
1	20	-10	100	-1,0	20	-15	225	-1,5	1,5
2	21	-9	81	-0,9	20	-15	225	-1,5	1,4
3	22	-8	64	-0,8	25	10	100	-1,0	0,8
…	…	..	…	…	…	…	…	…	…
100	50	20	400	2,0	50	15	225	1,5	3,0
Σ	3000	—	10000	—	3500	—	10000	—	70,0
Среднее	30	—		—	35	—		—	0,7

Как
видно, полученное среднее произведение
нормированных отклонений по признаку-фактору
и признаку-результату
представляет
собой коэффициент парной корреляции
между этими признаками. Поскольку этот
коэффициент положительный, то взаимосвязь
между признаками прямая, а величина
коэффициента корреляции (r
= 0,7) указывает на среднюю меру зависимости
годового удоя одной коровы от урожайности
сена многолетних трав.

Необходимо
иметь в виду, что абсолютная величина
коэффициента корреляции, как и
корреляционного отношения, может
колебаться от 0 до 1, а с учетом направления
связи
– находиться
в пределах от –
1
до 1. При этом чем ближе коэффициент
корреляции к единице (отрицательной
или положительной), тем теснее находятся
признаки во взаимосвязи.

Расчет
коэффициента корреляции по основной
формуле 11.2 хотя и дает довольно точный
результат, но отличается повышенной
трудоемкостью вычисления. Поэтому для
измерения степени тесноты связи между
факторным и результативным признаками
можно рекомендовать формулу, предложенную
К. Пирсоном:

,

(11.3)

где
r
_xy
– коэффициент прямолинейной парной
корреляции;
– среднее произведение факторного и
результативного признаков:– среднее значение соответственного
факторного и результативного признаков,–– средние квадратические отклонения
признака-фактора и признака-результата.

При
расчете коэффициента прямолинейной
парной корреляции по формуле 11.3 в общем
виде можно воспользоваться макетом
вспомогательной табл. 11.2.

Т а б
л и ц а 11.2. Схема
расчета вспомогательных показателей

Что такое корреляционная диаграмма?

Любой анализ начинается со сбора информации. Чем ее больше, тем точнее полученный в конечном итоге результат. В вышеприведенном примере у нас есть две дисциплины, по которым школьникам нужно сдать экзамен. Показатель успешности на них – это оценка. Корреляционно-регрессионный анализ показывает, влияет ли результат по одному предмету на баллы, набранные на втором экзамене. Для того чтобы ответить на этот вопрос, необходимо проанализировать оценки всех учеников на параллели. Но для начала нужно определиться с зависимой переменной

В данном случае это не так важно. Допустим, экзамен по математике проходил раньше

Баллы по нему – это независимая переменная (откладываются по оси абсцисс). Английский язык стоит в расписании позже. Поэтому оценки по нему – это зависимая переменная (откладываются по оси ординат). Чем больше полученный таким образом график похож на прямую линию, тем сильнее линейная корреляция между двумя избранными величинами. Это означает, что отличники в математике с большой долей вероятности получат пятерки на экзамене по английскому.

Настройка параметров брандмауэра

В левой панели присутствуют две ссылки:

• Изменение параметров уведомления
• Включение и отключение брандмауэра Windows

Обе ссылки открывают окно настройки параметров.

Для каждого профиля можно задать собственный набор параметров. Если брандмауэр включен, логично также включить уведомления о блокировке новой программы, чтобы ее поведение не вызывало у вас недоумения в случае блокировки. В диалоговом окне блокировки также имеется возможность разрешить или заблокировать программу для каждого профиля.

Сброс настроек брандмауэра

Чтобы восстановить стандартные значения брандмауэра, щелкните Восстановить умолчания в левой панели. В открывшемся окне подтвердите свое желание вернуть все на круги своя.

Корреляционная решетка

Корреляционная взаимосвязь может иметь один или несколько факторов-признаков, обладать положительной или отрицательной направленностью, быть прямолинейной или криволинейной (в зависимости от выражения). Определить, к какому именно типу относится связь, можно с помощью корреляционной решетки. Ее строят в пределах прямоугольных осей координат.

Частоты, размещенные близко к диагоналям, свидетельствуют о высокой взаимосвязи признаков. Частоты, размещенные близко к диагонали, проходящей через левый нижний и правый верхний углы, говорят о положительном направлении, а проходящие через верхний левый и правый нижний угол – о противоположном направлении. Частоты, расположенные в форме дуги, свидетельствуют о криволинейной взаимосвязи, а беспорядочно разбросанные – об отсутствии взаимосвязи вообще.

Основной метод корреляционного анализа – это линейный коэффициент корреляции. Он может принимать значение от -1 до +1. Чем ближе значение к 1, тем сильнее связь между фактором и результатом. Положительные значения говорят о прямой взаимосвязи, а отрицательные – об обратной. Коэффициент принимает значение «ноль» в том случае, если между признаками отсутствует взаимосвязь.

Пошаговая регрессия

_12mijxjxiy

На втором шаге строится уравнение регрессии с одной переменной, имеющей максимальный по абсолютной величине парный коэффициент корреляции с результативным признаком.

На третьем шаге в модель вводится новая переменная, имеющая наибольшее по абсолютной величине значение частного коэффициента корреляции с зависимой переменной при фиксированном влиянии ранее введенной переменной.
При введении в модель дополнительного фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит, т. е. коэффициент множественной детерминации увеличивается незначительно, то ввод нового фактора признается нецелесообразным.

Пример №1. По 20 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x1 (% от стоимости фондов на конец года) и от ввода в действие новых основных фондов x2 (%).

Y	X1	X2
6	10	3,5
6	12	3,6
7	15	3,9
7	17	4,1
7	18	4,2
8	19	4,5
8	19	5,3
9	20	5,3
9	20	5,6
10	21	6
10	21	6,3
11	22	6,4
11	23	7
12	25	7,5
12	28	7,9
13	30	8,2
13	31	8,4
14	31	8,6
14	35	9,5
15	36	10

Требуется:

1. Построить корреляционное поле между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации. Выдвинуть гипотезу о тесноте и виде зависимости между показателями X1 и Y .
2. Оценить тесноту линейной связи между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации с надежностью 0,9.
3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости выработки продукции на одного работника от удельного веса рабочих высокой квалификации.
4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,9 и построить для них доверительные интервалы.
5. Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,9.
6. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих.
7. Рассчитать коэффициенты линейного уравнения множественной регрессии и пояснить экономический смысл его параметров.
8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 и построить для них доверительные интервалы.
9. Найти коэффициенты парной и частной корреляции. Проанализировать их.
10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
11. С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,9.
12. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов составляет 5%.
13. Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты.

Решение проводим с помощью калькулятора. Далее приводится ход решения п.13.

Матрица парных коэффициентов корреляции R:

—	y	x1	x2
y	1	0.97	0.991
x1	0.97	1	0.977
x2	0.991	0.977	1

_{ixjxix1 x2yxiyx1критнаблкритyx2наблкритx1x22}Тестирование и устранение мультиколлинеарности222_табл2_табл2Определяем обратную матрицу-1

D =	55,365 -2,256 -52,656 -2,256 22,386 -19,642 -52,656 -19,642 72,373

_{kk12kТабл12Табл1табл2табл13табл2}Частные коэффициенты корреляции_{ijyx1 /x2критнабл121yx2 /x1наблкрит21212}

Пример №2. По 30 наблюдениям матрица парных коэффициентов корреляции оказалась следующей:

	y	x1	x2	x3
y	1,0
x1	0,30	1,0
x2	0,60	0,10	1,0
x3	0,40	0,15	0,80	1,0

уравнение регрессии в стандартном масштабе

Критерии и методы

КРИТЕРИЙ СПИРМЕНА

Коэффициент ранговой корреляции Спирмена – это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.

Чарльз Эдвард Спирмен

1. История разработки коэффициента ранговой корреляции

Данный критерий был разработан и предложен для проведения корреляционного анализа в 1904 году Чарльзом Эдвардом Спирменом, английским психологом, профессором Лондонского и Честерфилдского университетов.

2. Для чего используется коэффициент Спирмена?

Коэффициент ранговой корреляции Спирмена используется для выявления и оценки тесноты связи между двумя рядами сопоставляемых количественных показателей. В том случае, если ранги показателей, упорядоченных по степени возрастания или убывания, в большинстве случаев совпадают (большему значению одного показателя соответствует большее значение другого показателя — например, при сопоставлении роста пациента и его массы тела), делается вывод о наличии прямой корреляционной связи. Если ранги показателей имеют противоположную направленность (большему значению одного показателя соответствует меньшее значение другого — например, при сопоставлении возраста и частоты сердечных сокращений), то говорят об обратной связи между показателями.

1. Коэффициент корреляции Спирмена обладает следующими свойствами:
2. Коэффициент корреляции может принимать значения от минус единицы до единицы, причем при rs=1 имеет место строго прямая связь, а при rs= -1 – строго обратная связь.
3. Если коэффициент корреляции отрицательный, то имеет место обратная связь, если положительный, то – прямая связь.
4. Если коэффициент корреляции равен нулю, то связь между величинами практически отсутствует.
5. Чем ближе модуль коэффициента корреляции к единице, тем более сильной является связь между измеряемыми величинами.

3. В каких случаях можно использовать коэффициент Спирмена?

В связи с тем, что коэффициент является методом непараметрического анализа, проверка на нормальность распределения не требуется.

Сопоставляемые показатели могут быть измерены как в непрерывной шкале (например, число эритроцитов в 1 мкл крови), так и в порядковой (например, баллы экспертной оценки от 1 до 5).

Эффективность и качество оценки методом Спирмена снижается, если разница между различными значениями какой-либо из измеряемых величин достаточно велика. Не рекомендуется использовать коэффициент Спирмена, если имеет место неравномерное распределение значений измеряемой величины.

4. Как рассчитать коэффициент Спирмена?

Расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:

1. Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию или убыванию.
2. Определить разности рангов каждой пары сопоставляемых значений (d).
3. Возвести в квадрат каждую разность и суммировать полученные результаты.
4. Вычислить коэффициент корреляции рангов по формуле:

Определить статистическую значимость коэффициента при помощи t-критерия, рассчитанного по следующей формуле:

5. Как интерпретировать значение коэффициента Спирмена?

При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 — признаком слабой тесноты связи; значения более 0,3, но менее 0,7 — признаком умеренной тесноты связи, а значения 0,7 и более — признаком высокой тесноты связи.

Также для оценки тесноты связи может использоваться шкала Чеддока:

_xy
Теснота (сила) корреляционной связи
менее 0.3
слабая
от 0.3 до 0.5
умеренная
от 0.5 до 0.7
заметная
от 0.7 до 0.9
высокая
более 0.9
весьма высокая

Статистическая значимость полученного коэффициента оценивается при помощи t-критерия Стьюдента. Если расчитанное значение t-критерия меньше табличного при заданном числе степеней свободы, статистическая значимость наблюдаемой взаимосвязи — отсутствует. Если больше, то корреляционная связь считается статистически значимой.

Сфера использования понятия

Корреляция широко распространена в разных видах деятельности с целью обработки массивов статистических данных. Это касается, прежде всего, таких наук, как:

• экономика;
• математика;
• астрофизика;
• психология;
• социология и др.

Отдельно стоит выделить возможность применения корреляции в некоторых важных для человечества сферах деятельности. Это касается металловедения, агрохимии, биометрического анализа и биологии. В разных типах прикладных отраслей принято использовать предельные границы интервалов для оценки тесноты или же значимости связи.

Распространение использования метода корреляции обусловлено такими факторами, как:

• простота подсчета;
• отсутствие необходимости наличия специальной подготовки.

Интерпретация корреляции тоже под силы практически любому человеку. Именно поэтому данный метод так широко используется в различных сферах, где требуется анализ тех или иных статистических данных.

Hard Reset средствами самой системы Android

Регрессионный анализ в MS Excel

Для того чтобы вычислить уравнение линейной регрессии, описывающие взаимосвязь между факторами и результатом, в MS Excel применяется статистическая функция «Линейн». Для того чтобы ее использовать, необходимо:

1. Выделить пустую область, в которую будут выведены результаты анализа.
2. Открыть «Мастер функций», в нем найти категорию «Статистические», а в ней функцию «Линейн» и нажать ОК.
3. В поле «Известные значения у ввести диапазон анализируемых результатов, в поле «Известные значения х – диапазон анализируемых факторов.
4. В поле «Константа» указывается присутствие свободного члена уравнения (1 – да, 0 – нет), а в поле «Статистика» – необходимость вывода дополнительных сведений (1 – появится дополнительная информация, 0 – появятся только оценки параметров). По умолчанию можно указывать в обоих полях 1.
5. Нажать кнопку ОК.

Вверху ранее выделенной области появится начальный элемент таблицы. Для того чтобы раскрыть все данные, необходимо нажать F2, а потом одновременно комбинацию клавиш Ctrl + Shift + Enter.

В итоге регрессионная информация будет изображаться в качестве таблицы из двух столбцов и пяти строк:

	Столбец 1	Столбец 2
Строка 1	Коэффициент b	Коэффициент a
Строка 2	Среднеквадратическое отклонение b	Среднеквадратическое отклонение a
Строка 3	Коэффициент детерминации	Среднеквадратическое отклонение y
Строка 4	F-статистика	Число степеней свободы
Строка 5	Регрессионная сумма квадратов	Остаточная сумма квадратов

Полученные результаты необходимо подставить в линейное уравнение регрессии, которое выглядит следующим образом: y = a + bx. В качестве коэффициента a подставляется значение из ячейки на пересечении строки 1 и столбца 2. В качестве коэффициента b – значение на пересечение строки 1 и столбца 1.

Коэффициент детерминации говорит о том, какая часть результата объясняется с помощью исследуемого фактора. Оставшаяся часть результатов определяется факторами, неучтенными в линейной модели.

Шесть тысяч четыреста пятьдесят три рубля шестьдесят три копейки

Для чего нужна подпись

Корреляционно-регрессионный анализ

На практике эти две методики часто применяются вместе.

Пример:

1. Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
2. Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
3. Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
4. Жмем «Закрыть».

Теперь стали видны и данные регрессионного анализа.

Для того чтобы посчитать коэффициент корреляции r- Пирсона в эксель нужно

1.Открыть программу Excel

2.Создать столбцы с данными. В нашем примере мы будем считать взаимосвязь, или корреляцию, между агрессивностью и неуверенностью в себе у детей-первоклассников. В эксперименте участвовали 30 детей, данные представлены в таблице эксель:

1 столбик — № испытуемого

2 столбик — агрессивность в баллах

3 столбик — неуверенность в себе в баллах

3.Затем необходимо выбрать пустую ячейку рядом с таблицей и нажать на значок f(x) в панели Excel

4.Откроется меню функций, среди категорий необходимо выбрать Статистические, а затем среди списка функций по алфавиту найти КОРРЕЛ и нажать ОК

5.Затем откроется меню аргументов функции, которое позволит выбрать нужные нам столбики с данными. Для выбора первого столбика Агрессивность нужно нажать на синюю кнопочку у строки Массив1 

6.Выберем данные для  Массива1 из столбика Агрессивность и нажмем на синюю кнопочку в диалоговом окне

7. Затем аналогично Массиву 1 нажмём на синюю кнопочку у строки Массив2 

8.Выберем данные для  Массива2 — столбик Неуверенность в себе и опять нажмем синюю кнопку, затем ОК

9.Вот, коэффициент корреляции r-Пирсона посчитан и записан в выбранной ячейке.В нашем случае он положительный и приблизительно равен . Это говорит об умеренной положительной связи между агрессивностью и неуверенностью в себе у детей-первоклассников

Таким образом, статистическим выводом эксперимента будет: r = 0,225, выявлена умеренная положительная взаимосвязь между переменными агрессивность и неуверенность в себе.

Содержательным выводом будет следующее заключение: у первоклассников неуверенность в себе приводит к агрессивному поведению, для коррекции агрессии необходимо работать с самооценкой ребенка, диагностировать её уровень и провести коррекционные мероприятия по её повышению.

В некоторых исследованиях требуется указывать р-уровень значимости коэффициента корреляции, однако программа Excel, в отличие от SPSS,  не предоставляет такой возможности. Ничего страшного, есть таблицы критических значений корреляций (А.Д. Наследов).

Также Вы можете построить в эксель линию регрессии и приложить её к результатам исследования.

Этапы анализа

Корреляционно-регрессионный анализ экономических процессов разделяется на несколько этапов:

1. Определение аргументов и предварительная обработка условной информации.
2. Определение тесноты и формы взаимосвязи между несколькими признаками.
3. Моделирование представленного экономического процесса и анализ полученной модели.
4. Применение конечных результатов для усовершенствования планирования и менеджмента модели.

Статистическую однородность информации можно определить с помощью двух приемов. Для начала необходимо определить и откинуть значение факторов, резко отличающихся от всех величин. Потом осуществляется статистическое исследование однородности с помощью проверки независимости выборки и ее принадлежности к единственной совокупности с нормальным распределением.

Модель регрессии определяется через метод наименьших квадратов, благодаря которому обеспечивается самое лучшее приближение оценки результата, определенного через уравнение регрессии, к его факторам.

Корреляционный анализ по Спирмену – практическое применение в торговых стратегиях

Корреляционный анализ Спирмена, оценивает рыночную ситуацию с точки зрения ее цикличности, то есть чередования периодов роста и падения. Получается, что трейдеры могут использовать его в торговых стратегиях в качестве определителя трендовых изменений – чем значение коэффициента Спирмена выше, тем больше вероятность того, что произойдет смена тенденции.

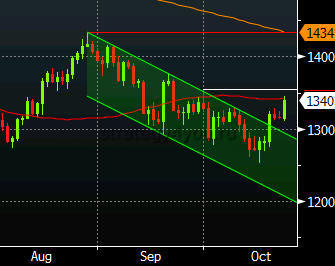
Ориентируясь на сигналы индикатора (осциллятора), использующего в своей работе коэффициент Спирмена можно выстроить определенно выгодную торговлю. При этом, значимыми уровнями здесь будут максимальные и минимальные значения, выдаваемые инструментом, которые называются уровнями статистической значимости, как на примере ниже.

Еще одно практическое применение корреляционный анализ по Спирмену нашел в так называемом парном трейдинге. Называется он так по той причине, что ведется одновременная торговля парами коррелируемых инструментов (опционы, валютные пары, фьючерсные контракты, индексы). То есть парный трейдинг является торговой стратегией основанной на феномене корреляции торговых инструментов.

В свою очередь, различают два вида корреляции в анализе рынка по Спирмену:

• прямая
• и обратная.

На примере ниже мы видим графики прямой или положительной корреляции валютных пар GBP/USD и EUR/USD и отрицательной или обратной корреляции пар USD/CHF и EUR/USD.

Необходимо отметить, что все пары валют между собой связаны фундаментальными факторами, поэтому примеров их корреляции можно привести очень много, но для парного трейдинга использовать можно не все. Здесь используются лишь те инструменты, степень корреляции которых достаточно высока.

Для подбора таких пар, можно воспользоваться специальными онлайн сервисами, как на примере ниже.

Синими кружками обозначена обратная корреляция, красными – прямая. Теперь давайте рассмотрим, как же происходит торговля по стратегии парного трейдинга, в которой применяется корреляционный анализ по Спирмену.

Первым делом, следует определиться с входом. Вход в сделку необходимо производить лишь убедившись, что коррелируемые пары разошлись по отношению к друг к другу максимально. Чтобы это сделать отмотайте график назад на 6 месяцев и вычислите насколько пунктов было расхождение. После этого определите среднее значение расхождения, по которому будете рассматривать возможный вход.

К примеру, среднее расхождение получилось 80 пунктов, значит рассматривать следует лишь те сделки расхождение между парами которых было как минимум 80 пунктов.

ТОП БРОКЕРОВ, ПРИЗНАННЫХ НЕЗАВИСИМЫМИ РЕЙТИНГАМИ

*БО. Не требуется верификация! | обзор/отзывы | НАЧАТЬ ТОРГОВЛЮ С 10$
*БО. Сделки от 60 рублей. | обзор/отзывы | НАЧАТЬ С 600 ₽

ЛУЧШИЕ ФОРЕКС БРОКЕРЫ ПО ДАННЫМ «ИНТЕРФАКС»

2007 год. FinaCom.   КОПИРОВАТЬ СДЕЛКИ ТРЕЙДЕРОВ | обзор/отзывы
1998 год. FCA, НАУФОР. | +20% ПО КЕШБЭКУ | обзор/отзывы
2007 год. БОНУС $1500 НА СЧЕТ. |
STARTUP BONUS $1500 | обзор/отзывы
2007 год. The FC.   ВЫБЕРИТЕ 10 ИЛИ 20$ НА СЧЕТ | обзор / отзывы

Далее определяемся с правилами входа, а также выхода из позиций. Открываем сразу две позиции, как только расхождение достигает своего максимума – более дорогая валюта (находится сверху) продаем, а более дешевую (снизу), соответственно покупаем. Сразу оговоримся, что в данной стратегии стоп приказы не применяются. Выход осуществляется, когда графики пар валют пересекутся в точке нуля.

Во избежание накапливания размера убытков, если расхождение коррелируемых инструментов будет продолжаться, можно применить локирование.

При этом, если цена начнет двигаться в нужном Вам направлении необходимо вовремя произвести разлокирование позиций.

Для данной стратегии в основу которой положен корреляционный анализ, наилучшим образом подходят торговые инструменты имеющие высокую степень корреляции (EUR/USD и GBP/USD, EUR/AUD и EUR/NZD, AUD/USD и NZD/USD, контракты CFD и тому подобные).

Касательно таймфрейма, то рекомендовано выбирать временные промежутки от М5 до Н1, но запомните, что чем выше интервал времени, тем реже появляется сигнал, хотя Take Profit при этом будет больше.

Применение корреляции Спирмена на рынке Форекс

Отображение результатов

Результаты корреляционного анализа могут быть представлены в текстовом и графическом видах. В первом случае они представляются как коэффициент корреляции, во втором — в виде диаграммы разброса.

При отсутствии корреляции между параметрами точки на диаграмме расположены хаотично, средняя степень связи характеризуется большей степенью упорядоченности и характеризуется более-менее равномерной удаленностью нанесенных отметок от медианы. Сильная связь стремится к прямой и при r=1 точечный график представляет собой ровную линию. Обратная корреляция отличается направленностью графика из левого верхнего в нижний правый, прямая — из нижнего левого в верхний правый угол.

Корреляционно-регрессионный анализ: параметры созданной модели

Самыми главными факторами, определяющими характеристики модели, принято считать:

• Коэффициенты парной корреляции (демонстрируют силу взаимосвязи двух факторов).
• Коэффициент множественной корреляции (определяет взаимосвязь результата и факторов).
• Коэффициенты частной детерминации (показывают влияние вариации аргумента на вариацию искомого признака).
• Коэффициент множественной детерминации (показывает удельный вес всех аргументов на вариацию искомого признака).
• Частные коэффициенты эластичности (характеризуют влияние факторов на результат, выраженное в едином масштабе в процентах).

Коэффициент корреляции

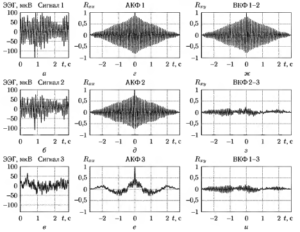Рисунок 4. Сравнение автокорреляционной функции (АКФ) и кросскорреляционной функции (ВКФ) для трех разных отведений

Значение корреляционного анализа состоит в нахождении автокорреляционной функции, которая показывает преобладающие ритмы, или взаимно-корреляционной функции, отражающей связь фрагмента обрабатываемого сигнала и эталона сигнала без помех и шумов или же связь между двумя неочищенными сигналами. (рис. 4) Биомедицинские сигналы относятся к квазипериодическим сигналам. ЭЭГ-сигналы содержат эпохи, имеющие схожие друг с другом характеристики. Эпоха ЭЭГ-сигнала – это произвольно выделенный период времени в записи ЭЭГ (чаще всего составляет 10 с.) В качестве эталона какой-либо эпохи ЭЭГ-сигнала используется либо стандартный фрагмент данного сигнала, свободный от помех и шумов, либо искусственно созданная модель стандартного фрагмента ЭЭГ-сигнала, построенная на основе заранее известных данных о форме и амплитудно-временных характеристик “чистого” фрагмента. Сравнение автокорреляционной функции (АКФ) и кросскорреляционной функции (ВКФ) для трех разных отведений представлено на рис. 4.  График под буквой г изображает автокорреляционную функцию фрагмента а. Подобная функция графика свидетельствует о том, что сходство двух эпох данного сигнала сходит на ноль относительно медленно. Следовательно, мы можем сделать вывод о периодичности процессов, протекающих в данном отведении, т.к. отдельные его фрагменты достаточно сильно схожи друг с другом. Аналогичные выводы можно сделать и о сигнале на графике б, опираясь на его функцию, обозначенную буквой д.

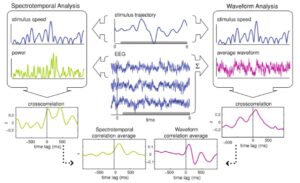Рисунок 5. Применение корреляционного анализа к обработке ЭЭГ-сигнала

С другой стороны, график в, автокорреляционная функция которого изображена на рисунке е, изображает хаотический процесс, отдельные фрагменты которого не подобны друг другу. Об этом свидетельствует крайне быстрое затухание его автокорреляционной функции. Т.о. процессы, протекающие в данном отведении, непериодичны, т.к. отдельные фрагменты графика мало схожи друг с другом.

График ж изображает кросс-корреляционную функцию между сигналами а и б. Ее медленное затухание свидетельствует о наличии взаимовлияния фрагментов а и б. График з и график и отражают кросс-корреляционную функцию между сигналами б–в и а–в соответственно. Поскольку затухание графика происходит достаточно быстро, мы можем сделать вывод о том, что между данными отрезками ЭЭГ-сигнала отсутствует существенная взаимосвязь. 

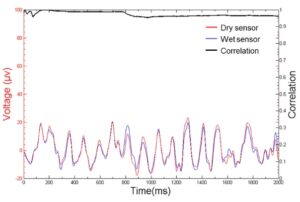Рисунок 6. Результат сравнения графиков напряжения при использовании сухих и влажных электродов

Корреляционный анализ применительно к исправлению графика ЭЭГ можно изобразить так: в центре иллюстрации приведено два графика – график воздействия стимула сверху (синий цвет) и фрагмент ЭЭГ снизу (синий цвет).  (рис. 5)

В правой части иллюстрации изображены графики скорости воздействия стимула (синий цвет) и средней формы волны (розовый цвет). Последний был получен путем суммации изначальных ЭЭГ-графиков. Их также подвергли кросскорелляционному анализу, результат которого приведен ниже (розовый цвет). Затем, используя полученные данные о корреляции, был построен исправленный график ЭЭГ-сигнала (розовый цвет).

В левой части изображены графики скорости воздействия стимула (синий цвет) и мощности ЭЭГ (зеленый цвет). Их подвергли кросскорелляционному анализу, результат которого приведен ниже (зеленый цвет). Затем, используя полученные данные о корреляции, был построен исправленный график ЭЭГ-сигнала (зеленый цвет).

В случае, изображенном на рис. 6, сравниваются графики напряжения при использовании сухих (красный) и влажных (синий) электродов. Степень корреляции результатов представлена в виде графика черного цвета в верхней части изображения.

Условия использования метода

Результативные факторы зависят от одного до нескольких факторов. Метод корреляционного анализа может применяться в том случае, если имеется большое количество наблюдений о величине результативных и факторных показателей (факторов), при этом исследуемые факторы должны быть количественными и отражаться в конкретных источниках. Первое может определяться нормальным законом — в этом случае результатом корреляционного анализа выступают коэффициенты корреляции Пирсона, либо, в случае, если признаки не подчиняются этому закону, используется коэффициент ранговой корреляции Спирмена.

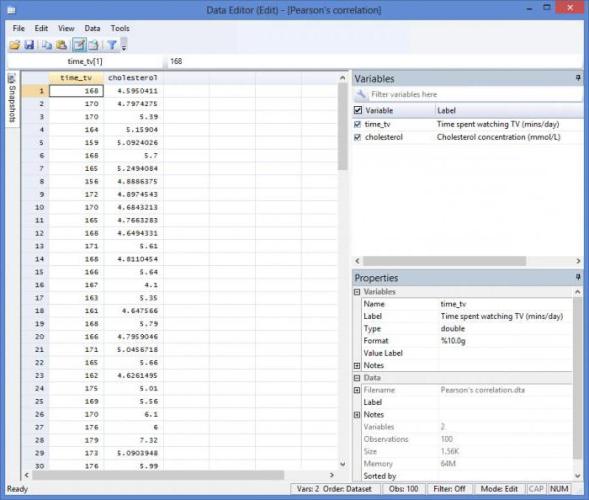
Программное обеспечение анализа

Для облегчения расчетов можно проводить корреляционный анализ в Excel. В данной программе существует ряд инструментов, помогающих облегчить расчеты. Среди них функция «Корреляция», позволяющая сформировать матрицу из коэффициентов и разных параметров. Она изображается в форме таблицы. В качестве столбцов и строк используются корреляционные коэффициенты. На основе полученных данных таблицы необходимо будет провести корреляционный анализ. Пример последовательности проведения анализа:

1. В команде «Сервис» выбрать пункт «Анализ данных».
2. В качестве инструмента анализа выбрать пункт «Корреляция».
3. В появившемся окне в строке «Входной интервал» указать диапазон анализируемых данных, выбрать пункт «Группировка» в строке «Параметры вывода», ввести диапазон вывода результатов и нажать «ОК».

В результате получится корреляционная матрица, расположенная в диапазоне вывода. Внутри будет указан коэффициент линейной корреляции, оценивающий тесноту и форму связи между показателями.

Множественная корреляция, её коэффициент

Множественная корреляция — это вероятностная зависимость между одной величиной с
одной стороны, и одновременно несколькими другими ,
с другой стороны.
То есть, в отличие от парной корреляции, при которой
на изменения зависимой (результирующей) переменной влияет одна независимая (объясняющая) переменная,
при множественной корреляции независимых (объясняющих) переменных две или больше.

Цель корреляционного анализа в случае множественной корреляции — установить, есть ли зависимость между
переменными и насколько тесно связаны между собой зависимая переменная, с одной стороны, и независимые
переменные, с другой стороны, и зависят ли друг от друга независимые переменные .

Для того чтобы можно было бы применять модель множественной линейной регрессии, прежде, при анализе
множественной корреляции должны быть установлены следующие факты:

• зависимая переменная тесно зависит от независимых переменных (тесноту связи, как и в случае
  парной корреляции, показывают );
• нет тесной зависимости между независимыми переменными.

Коэффициент множественной корреляции в случае двухфакторной корреляции рассчитывается по следующей формуле:

.

Коэффициенты множественной корреляции между зависимой переменной
и независимыми переменными
записываются в корреляционную матрицу:

Пример 1. Аналитик предприятия решил проверить факторы, которые
влияют на размер заработной платы сотрудников . Предварительно
в качестве объясняющих факторов выбраны: возраст сотрудника ,
стаж работы , оценка теста для приёма
на работу и число подчинённых
сотрудников . Случайно были выбраны
200 сотрудников, данные которых были обобщены. В результате была получена следующая корреляционная матрица:

	1
	-0,27	1
	0,78	-0,63	1
	-0,83	0,47	-0,89	1
	0,65	-0,46	0,17	-0,21	1

Установить, какие переменные можно выбрать как независимые, для того, чтобы далее
можно было бы строить модель множественной регрессии.

Решение.

Корреляционная матрица показывает, что между переменными:

• и — слабая линейная связь: -0,27;
• и — средне тесная положительная линейная связь: 0,78;
• и — тесная отрицательная линейная связь: -0,83;
• и — средне тесная линейная связь: 0,65;
• и — тесная отрицательная линейная связь: -0,89;
• и — слабая линейная связь: 0,17;
• и — слабая линейная связь: -0,21.

Таким образом, не следует включать в число переменных, влияющих на размер заработной
платы возраст сотрудников . Так как
между независимыми переменными и
установлена тесная отрицательная связь,
не включаем в число переменных, влияющих на размер заработной платы стаж работы .
Выбираем в качестве независимых переменных оценку теста для приёма
на работу и число подчинённых
сотрудников .

Чтобы установить тесноту связи между заработной платой сотрудников ,
с одной стороны, и оценкой теста для приёма
на работу и числом подчинённых
сотрудников , с другой стороны,
вычислим коэффициент множественной (двухфакторной) корреляции:

Таким образом, между заработной платой сотрудников, с одной стороны, и
оценкой теста для приёма на работу и числом подчинённых, с другой стороны, существует тесная линейная
связь.

Как показывает пример выше, в исследованиях поведения человека,
как и во многих других направлениях, важно установить, какие факторы из многих действительно влияют на
результат при учете влияния всех остальных факторов