Как пишется значок корня на клавиатуре

Содержание:

Как набирать
- Знак корня на клавиатуре
- Способы набора символа в Ворде
Примечания
Способ 3: «Командная строка»
Дискриминант: формула корней квадратного уравнения
Как написать корень на клавиатуре
- Как найти знак корня на клавиатуре?
Квадратные корни из натуральных чисел
Применение
Способы набора на пк и ноутбуке
Зачем нужно знать словообразование?
Способы набора на пк и ноутбуке

Как набирать

Знак корня на клавиатуре

В электронном виде этот символ может понадобиться как студентам, учителям, научным деятелям. Связано это может быть с докладом, проектом, рефератом и так далее. В стандартной раскладке клавиатуры нет символа квадратного корня, так как он не является популярным или часто используемым. Но его можно набрать и другими способами.

Самые распространённые программы для работы с документами – это пакет MS Office, в частности, Microsoft Word. Набрать квадратный корень в этой программе можно несколькими способами, которые по аналогии могут подойти и к другим программам, с небольшими различиями в интерфейсе.

Способы набора символа в Ворде

Можно использовать следующие варианты:

При помощи набора специального кода . В самом низу клавиатуры находится клавиша с названием Alt. Этих клавиш две, подойдёт любая из них. В правой части клавиатуры есть цифры, над которыми находится клавиша Num Lock. Эту клавишу нужно предварительно нажать, чтобы активировать цифры, находящиеся под ней. Затем зажимаем клавишу Alt и не отпуская клавишу, набираем: 251. После этого на экране появится нужный значок.
Ещё один способ связан с меню «вставка-символ». После того как будет найден нужный знак, его можно будет повторять, как ранее использованный. Его код в меню поиска — 221A, (латинская буква). Предварительно лучше включить Юникод.
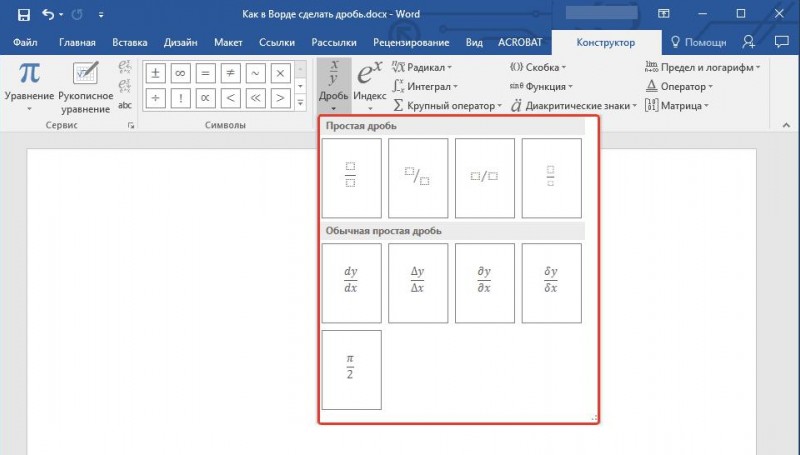
Самый «красивый» символ набирается с помощью компонента Microsoft Equation 3.0. Для этого надо зайти в «вставка-объект-Microsoft Equation 3.0», после чего найти там нужный знак и использовать его. При этом методе знак смотрится лучше всего, так как тут он отображается правильно с типографической и математической точки зрения.

Не получили ответ на свой вопрос? Предложите авторам тему.

Школьники или студенты в наше время часто работают в текстовом редакторе «Ворд». Однако ввиду недостаточной осведомленности некоторые задачи в нем они не способны выполнить. Особенно сложно работать с математическими символами, ведь на клавиатуре их недостаточно. В этой статье пойдет речь о знаке корня. Будет рассказано, как вставить его в документ. Продемонстрировано будет четыре разных способа, а по итогу прочтения статьи пользователь решит для себя сам, каким из них пользоваться.

Примечания

Сканави М. И. Элементарная математика. П. 1.11. С. 49.
↑ , с. 64.
Алгебраический (многозначный) корень в источниках часто называют просто корнем.
, Т. I, С. 35—36.
, с. 141—143.
Алгебра и начала анализа. Учебник для 10—11 классов, под ред. А. Н. Колмогорова. М.: Просвещение, 2002, С. 209.
↑ , с. 183.
, Т. I, С. 194, 198.
, с. 236—238.
, Т. I, С. 215.
, Т. I, С. 233, частный случай для μ=1n.{\displaystyle \mu ={\frac {1}{n}}.}.
Не путать с кратными интегралами. Их записи весьма похожи, но k{\displaystyle k}-й интеграл является неопределённым, в то время как k{\displaystyle k}-кратный интеграл — определённый.
, Том I, стр. 67, 131—132, 164, 166—167.
Алгебра. 9 класс. Учебник для общеобразовательных учреждений / Под ред. С. А. Теляковского. — Изд. 18-е. — М.: Просвещение, 2011. — С. 53. — ISBN 978-5-09-025168-6.
, с. 36—37.
Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — издание третье, стереотипное. — М.: Наука, 1976. — С. 68. — 591 с.
↑ , с. 96-99, 28—29.
Porteous, Ian R. Clifford Algebras and the Classical Groups. Cambridge, 1995, page 60.
См., например: Гантмахер Ф. Р. Теория матриц. М.: ГИТТЛ, 1953, С. 212—219, или: Воеводин В., Воеводин В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. Спб.: БХВ-Петербург, 2006.
См., например: Ершов Л. В., Райхмист Р. Б. Построение графиков функций. М.: Просвещение, 1984, или: Каплан И. А. Практические занятия по высшей математике. Харьков: Изд-во ХГУ, 1966.
См., например: Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. М.: Мир, 1983, или: Халмош П. Гильбертово пространство в задачах. М.: Мир, 1970.
, Том I, С. 42—46.
, Том I, С. 47.
, Том I, С. 169—171.
Башмакова И. Г. Становление алгебры (из истории математических идей). — М.: Знание, 1979. — С. 23. — (Новое в жизни, науке, технике. Математика, кибернетика, № 9).
, Том I, С. 275—276.
, Том I, С. 296—298.
, Том III, С. 56—59.
, Том III, С. 62.
Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Математическая логика, алгебра, теория чисел, теория вероятностей. — М.: Наука, 1978. — Т. I. — С. 58—66.
, Том I, С. 185.
Никифоровский В. А. Из истории алгебры XVI-XVII вв. — М.: Наука, 1979. — С. 81. — 208 с. — (История науки и техники).
Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник, изд. 3-е. — СПб.: ЛКИ, 2008. — С. 82. — 248 с. — ISBN 978-5-382-00839-4.

Как набрать на клавиатуре сердечко значок. как сделать сердце на клавиатуре

Способ 3: «Командная строка»

Как на клавиатуре написать значок евро

Дискриминант: формула корней квадратного уравнения

Извлечение корня любой степени в ms excel 2010

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Выводим формулу корней квадратного уравнения

Продолжим изучать формулу корней квадратного уравнения.

Пусть перед нами есть задача решить квадратное уравнение ax2 + bx + c = 0. Выполним ряд равносильных преобразований:

разделим обе части этого уравнения на отличное от нуля число a, после чего получим приведенное квадратное уравнение:
выделим полный квадрат левой части нового уравнения:
,

после чего уравнение примет вид
перенесем два последних слагаемых в правую часть и сменим знак на противоположный:
преобразуем выражение в правой части:

Так, мы пришли к уравнению , которое полностью равносильно исходному ax2 + bx + c = 0.

Отсюда выводы про корни уравнения :

И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части

При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D

По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько.

Повторим:

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения

Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней

Алгоритм решения квадратного уравнения ax2 + bx + c = 0:

вычислить его значение дискриминанта по формуле D = b2−4ac;
если дискриминант отрицательный, зафиксировать, что действительных корней нет;
если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = — b2/2a;
если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4×2 + 28x — 49 = 0.

Как решаем:

Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0
Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
Найдем корень
х = — 28/2(-4)

х = 3,5

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6×2 = 0.

Как решаем:

Произведем равносильные преобразования. Умножим обе части на −1
54 — 6×2 = 0 | *(-1)

6×2 — 54 = 0
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
6×2 = 54

х2 = 9

х = ±√9

х₁ = 3, х₂ = — 3

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x2— х = 0.

Как решаем:

Преобразуем уравнение так, чтобы появились множители
х(х — 1) = 0

х₁ = 0, х₂ = 1

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x2— 10 = 39.

Как решаем:

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
x2— 10 = 39

x2= 39 + 10

x2= 49

х = ±√49

х₁ = 7, х₂ = −7

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3×2— 4x+94 = 0.

Как решаем:

Найдем дискриминант по формуле
D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112
Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Приходите решать примеры на бытовых ситуациях, с красочными героями и в интерактивном формате. Запишите вашего ребенка на бесплатный пробный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.

Как написать корень на клавиатуре

Очень часто при наборе текстовых документов возникает необходимость написать символ, которого нет на клавиатуре.

Например, не редко возникает необходимость написать корень либо знак градуса. В данной статье мы рассмотрим сразу несколько способов, как можно написать корень на клавиатуре или без ее использования.

Если вам необходимо просто поставить знак корень, то это делается достаточно просто. Для этого необходимо воспользоваться комбинацией клавиш ALT+251. Данная комбинация клавиш нажимается следующим образом: сначала зажимаете клавишу ALT на клавиатуре, а потом не отпуская ALT набираете число 251 на дополнительном цифровом блоке (под клавишей Num Lock).

необходимо отметить, что число 251 необходимо набирать именно на дополнительном цифровом блоке, а Num Lock должен быть включен. Иначе комбинация клавиш ALT+251 не сработает. На скриншоте внизу показан индикатор сообщающий, что Num Lock включен.

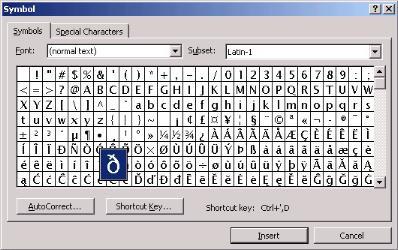
Кроме этого вы можете воспользоваться программой «Таблица символов», которая есть в любой версии Windows. С помощью этой программы можно вставить в текст знак корень или любой другой символ. Для того чтобы запустить «Таблицу символов» нажмите Windows-R и в открывшемся окне выполните команду «charmap.exe».

Либо воспользуйтесь поиском в меню «Пуск» и введите поисковый запрос «таблица символов».

После открытия «Таблицы символов» вам необходимо найти знак корень, нажать на кнопку «Выбрать», а потом на кнопку «Копировать». В результате выбранный вами символ будет скопирован в буфер обмена, и вы сможете вставить его в необходимое место вашего текста с помощью комбинации клавиш CTRL-V либо с помощью команды «Вставить».

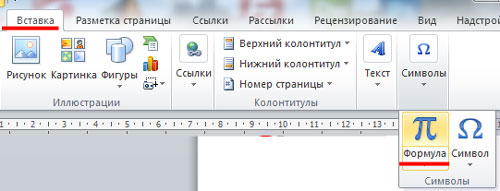
Если вы набираете текст в программе Word, то вы можете написать знак корень с помощью встроенного редактора формул. Для этого необходимо перейти на вкладку «Вставка», открыть там меню «Формула» и выбрать вариант «Вставить новую формулу».

В результате, в том месте, где был установлен ваш курсор появится рамка, подписанная как «Место для формулы».

После этого необходимо перейти на вкладку «Конструктор» и списке доступных символов выбрать знак корень.

Если все было сделано правильно, то в рамке для формул появится знак корень.

Как найти знак корня на клавиатуре?

Источник статьи: http://komza.ru/programmy/kak-napisat-koren-na-klaviature.html

Квадратные корни из натуральных чисел

Положительное число имеет два квадратных корня, один положительный, и отрицательный, которые противоположны друг другу. Когда речь идет о на квадратный корень из положительного целого числа, то, как правило , положительный квадратный корень , который имел в виду.

Квадратные корни из целого числа — это целые алгебраические числа, а точнее — квадратичные целые числа .

Квадратный корень из положительного целого числа — это произведение корней его простых множителей, потому что квадратный корень из произведения — это произведение квадратных корней из множителей. Поскольку необходимы только корни тех простых чисел, которые имеют нечетную степень при факторизации . Точнее, квадратный корень из разложения на простые множители равен
п2kзнак равнопk,{\ displaystyle {\ sqrt {p ^ {2k}}} = p ^ {k},}

п12е1+1⋯пk2еk+1пk+12еk+1…пп2епзнак равноп1е1…ппепп1…пk.{\ Displaystyle {\ sqrt {p_ {1} ^ {2e_ {1} +1} \ cdots p_ {k} ^ {2e_ {k} +1} p_ {k + 1} ^ {2e_ {k + 1}} \ dots p_ {n} ^ {2e_ {n}}}} = p_ {1} ^ {e_ {1}} \ dots p_ {n} ^ {e_ {n}} {\ sqrt {p_ {1} \ dots p_ {k}}}.}

В виде десятичных разложений

Квадратные корни из полных квадратов (например, 0, 1, 4, 9, 16) являются целыми числами . Во всех остальных случаях квадратные корни из положительных целых чисел являются иррациональными числами и, следовательно, имеют неповторяющиеся десятичные дроби в их десятичных представлениях . Десятичные приближения квадратных корней из первых нескольких натуральных чисел приведены в следующей таблице.

п	п,{\ displaystyle {\ sqrt {n}},} усечено до 50 знаков после запятой
1	1
2	1,4142135623 7309504880 1688724209 6980785696 7187537694
3	1.7320508075 6887729352 7446341505 8723669428 0525381038
4	2
5	2,2360679774 9978969640 9173668731 2762354406 1835961152
6	2.4494897427 8317809819 7284074705 8913919659 4748065667
7	2,6457513110 6459059050 1615753639 2604257102 5918308245
8	2,8284271247 4619009760 3377448419 3961571393 4375075389
9	3
10	3,1622776601 6837933199 8893544432 7185337195 5513932521

Как расширения в других системах счисления

Как и раньше, квадратные корни из полных квадратов (например, 1, 4, 9, 16) являются целыми числами. Во всех остальных случаях квадратные корни из положительных целых чисел являются иррациональными числами и, следовательно, имеют неповторяющиеся цифры в любой стандартной позиционной системе обозначений .

Квадратные корни из малых целых чисел используются в схемах хэш-функций SHA-1 и SHA-2, чтобы ничего не дать мне в числах в рукаве .

Как периодические непрерывные дроби

Один из самых интригующих результатов изучения иррациональных чисел как цепных дробей был получен Джозефом Луи Лагранжем c. 1780. Лагранж обнаружил, что представление квадратного корня из любого положительного целого числа, не являющегося квадратом, в виде непрерывной дроби является периодическим . То есть определенный образец частичных знаменателей бесконечно повторяется в непрерывной дроби. В каком-то смысле эти квадратные корни являются простейшими иррациональными числами, потому что они могут быть представлены простым повторяющимся шаблоном целых чисел.

2{\ displaystyle {\ sqrt {2}}}	=
3{\ displaystyle {\ sqrt {3}}}	=
4{\ displaystyle {\ sqrt {4}}}	=
5{\ displaystyle {\ sqrt {5}}}	=
6{\ displaystyle {\ sqrt {6}}}	=
7{\ displaystyle {\ sqrt {7}}}	=
8{\ displaystyle {\ sqrt {8}}}	=
9{\ displaystyle {\ sqrt {9}}}	=
10{\ displaystyle {\ sqrt {10}}}	=
11{\ displaystyle {\ sqrt {11}}}	=
12{\ displaystyle {\ sqrt {12}}}	=
13{\ displaystyle {\ sqrt {13}}}	=
14{\ displaystyle {\ sqrt {14}}}	=
15{\ displaystyle {\ sqrt {15}}}	=
16{\ displaystyle {\ sqrt {16}}}	=
17{\ displaystyle {\ sqrt {17}}}	=
18{\ displaystyle {\ sqrt {18}}}	=
19{\ displaystyle {\ sqrt {19}}}	=
20{\ displaystyle {\ sqrt {20}}}	=

Квадратная скобка обозначение , используемое выше , является краткой формой для непрерывной дроби. Написанная в более сложной алгебраической форме, простая непрерывная дробь для квадратного корня из 11, , выглядит так:

11знак равно3+13+16+13+16+13+⋱{\ displaystyle {\ sqrt {11}} = 3 + {\ cfrac {1} {3 + {\ cfrac {1} {6 + {\ cfrac {1} {3 + {\ cfrac {1} {6+ {) \ cfrac {1} {3+ \ ddots}}}}}}}}}}}

где двузначный образец {3, 6} повторяется снова и снова в частичных знаменателях. Так как 11 = 3 2 + 2 , выше, также идентичен следующие :

11знак равно3+26+26+26+26+26+⋱знак равно3+620-1-120-120-120-120-⋱.{\ displaystyle {\ sqrt {11}} = 3 + {\ cfrac {2} {6 + {\ cfrac {2} {6 + {\ cfrac {2} {6 + {\ cfrac {2} {6+ { \ cfrac {2} {6+ \ ddots}}}}}}}}} = 3 + {\ cfrac {6} {20-1 — {\ cfrac {1} {20 — {\ cfrac {1} { 20 — {\ cfrac {1} {20 — {\ cfrac {1} {20- \ ddots}}}}}}}}}}.}

Применение

Разумный вопрос, который рано или поздно возникает у человека, только начавшего изучать математику – зачем вообще нужен квадратный корень? Конечно, он, может, никогда и не пригодится уборщице тёте Люсе или дворнику дяде Васе, но для более образованного человека квадратный корень всё же нужен.

Начнём с того, что квадратный корень нужен для вычисления диагонали прямоугольника. Ну и что с того? – спросят многие. А с того, что это нужно для качественного ремонта, чтобы правильно и аккуратно разложить линолеум, сделать навесной потолок и для проведения многих других работ в сфере строительства.

Ведь дома и квартиры строят люди, вещи и материалы для ремонта изготавливают люди, либо машины, которыми управляют опять-таки люди. А человеку свойственно ошибаться. Поэтому вычисление квадратного корня может существенно сэкономить нервы и деньги при ремонте какого-либо помещения.

Квадратный корень также необходим физикам, математикам, программистам и другим профессионалам, чья профессия связана с вычислениями и наукой. Без подобных знаний наука стояла бы на месте. Однако даже простому человеку никогда не помешают базовые знания о корне. Ведь эти знания развивают мозг, заставляют его работать, образуя новые нейронные связи. Чем больше знаний в голове – тем больше человек запомнит.

Способы набора на пк и ноутбуке

Часто, чтобы поставить в текст радикал или запись с ним, используются сочетания букв. Sqrt, например, означает кв. корень, а cbrt – кубический. Но писать буквенные комбинации, слова неудобно. Кроме того, они не всем понятны.

Используем таблицу символов

Удобный инструмент, работающий в различных приложениях Microsoft Office, блокноте, – таблица символов.

Вызвать ее можно несколькими способами:

набрать в строке поиска название приложение;
вызвать командную строку сочетанием клавиш win + r, набрать charmap.exe. Вызов осуществляется, если последовательно кликнуть «пуск», «выполнить»;
зайти в пуск, перейти в стандартные программы, затем – служебные, выбрать искомое приложение.

Далее найти значок корня, последовательно щелкнуть выделить, копировать и вставить в нужное место.

Код символа

Простой метод вставить корень – использовать код.

включить цифровую клавиатуру, нажав NumLock;
нажать alt и, удерживая клавишу, набрать 251 с цифрового блока.

В случае с ноутом сделать нужно так:

внимательно посмотреть на клаву;
найти на буквенной части цифры. Они находятся под буквами в правой части – 2 под английской K, 5 – под I, 1 – под J;
включить функциональную клавишу, которая их активирует. Для этого кликнуть Fn и кнопку от F1 до F12 (зависит от ноутбука);
нажать альт и 251 с активированной клавы.

При работе с документом html, в программировании используются следующие значения:

Значок корня в уравнении

В документе можно написать не просто радикал, но и целое уравнение со степенью, неизвестным составляющим.

перейти во «Вставку»;
открыть раздел формул;
выбрать квадратное уравнение. Если нужен другой тип уравнения, вызвать функцию «вставить новую формулу»;
заполнить значения, в том числе степень над элементом в левой его части. Она может быть третьей, пятой, седьмой – любой.

Самостоятельно уравнение с х, корнем из некоего числа записывается и через инструмент «Объект» в меню «Вставка». После нажатия на объект перейти в Microsoft equation 3.0, «Шаблоны дробей и радикалов». В открывшемся конструкторе записать уравнение.

Шестнадцатеричный код

Для включения элемента может использоваться шестнадцатеричная система Юникод.

ввести кодовое значение. Квадратный корень обозначается 221A, кубический – 221B, четвертый – 221C. Буквы после цифр писать в латинской раскладке;
одновременно выжать сочетание Alt+X.

Способы набора символа в ворде

Чтобы поставить радикал в документе word, можно использовать большинство описанных методов.

скопировать элемент из другого текста, браузера, вставить;
использовать код+alt, код шестнадцатеричной системы;
через таблицу символов;
с помощью встроенного редактора формул. Для этого нажимают на раздел «Вставка», выбирают «Формула», жмут на «Вставить новую формулу». Появится надпись «Место для формулы», а в верхней панели инструментов – конструктор математических знаков. Остается выбрать значок и подкоренное выражение. Можно сразу выбрать значок со степенью 2, 3, 4, 5, даже 6;
через инструмент «Объект»;
изобразить значок в графическом редакторе – нарисовать галочку, одну сторону продлить. Перенести картинку в документ.

Зачем нужно знать словообразование?

Главная польза в том, что знание значений приставок и суффиксов значительно увеличивает количество слов, которые вы узнаете при чтении и слушании (особенно при чтении). Иначе говоря, увеличивается пассивный словарный запас.

Возьмем, к примеру, глагол to use – использовать. С помощью суффиксов из него образуются:

Прилагательное useful – полезный.
Прилагательное useless – бесполезный.
Существительное usage – использование.

Понимая значение суффиксов -ful, -less, -age, вы без труда поймете все три образованные от to use слова, даже если не знали их значение.

-ful и -less указывают на наличие или отсутствие качества: от слова care (забота, ) careful – осторожный, careless – беззаботный.
-age образует существительные от глаголов: leak (протекать) – leakage (утечка), pass (проходить) – passage (проход).

А почему пассивный словарный запас, почему не активный? Префиксы и суффиксы – это хорошие смысловые подсказки, но английская лексика так устроена (как и русская), что не к любому слову можно приделать любой аффикс.

Яркий пример – приставки in- и un-, имеющие значение отрицания: able – способный, unable – неспособный, stable – стабильный, instable – нестабильный. Приставки совершенно совпадают по смыслу, но вот когда какую нужно “приставлять” – это нужно запомнить. При чтении вы легко поймете смысл слов с inun-, но в речи можете и ошибиться.

Впрочем, это не так уж страшно. Уверен, что вас поймут, если вы скажете inable и unstable, перепутав приставки. Говоря по-русски, мы еще и не такие ошибки совершаем!

Способы набора на пк и ноутбуке

Используем таблицу символов

Удобный инструмент, работающий в различных приложениях Microsoft Office, блокноте, – таблица символов.

Вызвать ее можно несколькими способами:

набрать в строке поиска название приложение;
вызвать командную строку сочетанием клавиш win + r, набрать charmap.exe. Вызов осуществляется, если последовательно кликнуть «пуск», «выполнить»;
зайти в пуск, перейти в стандартные программы, затем – служебные, выбрать искомое приложение.

Далее найти значок корня, последовательно щелкнуть выделить, копировать и вставить в нужное место.

Код символа

Простой метод вставить корень – использовать код.

Алгоритм на пк:

включить цифровую клавиатуру, нажав NumLock;
нажать alt и, удерживая клавишу, набрать 251 с цифрового блока.

В случае с ноутом сделать нужно так:

внимательно посмотреть на клаву;
найти на буквенной части цифры. Они находятся под буквами в правой части – 2 под английской K, 5 – под I, 1 – под J;
включить функциональную клавишу, которая их активирует. Для этого кликнуть Fn и кнопку от F1 до F12 (зависит от ноутбука);
нажать альт и 251 с активированной клавы.

При работе с документом html, в программировании используются следующие значения:

&#8730 для квадратного корня;
&#8731 – кубического;
&#8732 – четвертого.

Значок корня в уравнении

В документе можно написать не просто радикал, но и целое уравнение со степенью, неизвестным составляющим.

Для этого:

перейти во «Вставку»;
открыть раздел формул;
выбрать квадратное уравнение. Если нужен другой тип уравнения, вызвать функцию «вставить новую формулу»;
заполнить значения, в том числе степень над элементом в левой его части. Она может быть третьей, пятой, седьмой – любой.

Шестнадцатеричный код

Для включения элемента может использоваться шестнадцатеричная система Юникод.

Работает так:

ввести кодовое значение. Квадратный корень обозначается 221A, кубический – 221B, четвертый – 221C. Буквы после цифр писать в латинской раскладке;
одновременно выжать сочетание Alt+X.

Способы набора символа в ворде

Чтобы поставить радикал в документе word, можно использовать большинство описанных методов.

Среди них:

скопировать элемент из другого текста, браузера, вставить;
использовать код+alt, код шестнадцатеричной системы;
через таблицу символов;
с помощью встроенного редактора формул. Для этого нажимают на раздел «Вставка», выбирают «Формула», жмут на «Вставить новую формулу». Появится надпись «Место для формулы», а в верхней панели инструментов – конструктор математических знаков. Остается выбрать значок и подкоренное выражение. Можно сразу выбрать значок со степенью 2, 3, 4, 5, даже 6;
через инструмент «Объект»;
изобразить значок в графическом редакторе – нарисовать галочку, одну сторону продлить. Перенести картинку в документ.